题目内容
10.如图,在Rt△ABC中,∠ABC=90°,DH垂直平分AB交AC于点E,连接BE、CD,且CD=CE.(1)如图1,求证:四边形BCDE是平行四边形;
(2)如图2,点F在AB上,且BF=BC,连接BD,若BD平分∠ABC,试判断DF与AC的位置关系,并证明你的结论.

分析 (1)根据线段垂直平分线性质得出AE=BE,∠AHE=∠BHE=90°,推出∠A=∠ABE,∠A+∠AEH=∠ABE+∠BEH=90°,求出∠AEH=∠ACB=∠BEH,求出∠D=∠BEH,∠CED=∠ACB,根据平行线的判定得出BE∥CD,BC∥ED,根据平行四边形的判定得出即可;
(2)求出HE=HF,根据SAS推出△DHF≌△AHE,根据全等得出∠A=∠FDH,求出∠EGD=90°即可.
解答 (1)证明:∵DH垂直平分AB交AC于点E,
∴AE=BE,∠AHE=∠BHE=90°,
∴∠A=∠ABE,∠A+∠AEH=∠ABE+∠BEH=90°,
∵∠ABC=90°,
∴∠A+∠ACB=90°,
∴∠AEH=∠ACB=∠BEH,
∵CE=CD,
∴∠D=∠CED,
∵∠AEH=∠CED,
∴∠D=∠BEH,∠CED=∠ACB,
∴BE∥CD,BC∥ED,
∴四边形BCDE是平行四边形;
(2)DF⊥AC,
证明:∵四边形BCDE是平行四边形,
∴DE=BC,
∵BC=BF,
∴BF=DE,
∵BD平分∠ABC,∠ABC=90°,
∴∠HBD=45°,
∵∠BHD=90°,
∴∠HBD=∠HDB=45°,
∴DH=BH=AH,
∴DH-DE=BH-BF,
∴HE=HF,
在△DHF和△AHE中
$\left\{\begin{array}{l}{DH=AH}\\{∠DHF=∠AHE}\\{HF=HE}\end{array}\right.$
∴△DHF≌△AHE,
∴∠A=∠FDH,
∵∠A+∠AEH=90°,∠DEC=∠AEH,
∴∠FDH+∠DEC=90°,
∴∠EGD=180°-90°=90°,
∴DF⊥AC.
点评 本题考查了平行四边形的性质和判定,全等三角形的性质和判定,等腰三角形的性质和判定的应用,能综合运用知识点进行推理是解此题的关键.

| A. | 盈利50元 | B. | 盈利100元 | C. | 亏损150元 | D. | 亏损100元 |
| 种植户 | 种植A类蔬菜面积 (亩) | 种植B类蔬菜面积 (单亩) | 总收入 (单位:元) |
| 甲 | 3 | 2 | 28000 |
| 乙 | 2 | 1 | 16500 |
(1)求A、B两类蔬菜每亩平均收入格式多少元?
(2)某种植户准备租18亩地用来种植A、B两类蔬菜,为了使总收入不低于96000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所用租地方案.
 已知△ABC中,∠A=90°,AB=AC,D为BC的中点.
已知△ABC中,∠A=90°,AB=AC,D为BC的中点. 如图所示,一棵大树在一次强烈的地震中于C处折断倒下,树顶落在地面B处,测得B处与树的底端A相距25米,∠ABC=24°.
如图所示,一棵大树在一次强烈的地震中于C处折断倒下,树顶落在地面B处,测得B处与树的底端A相距25米,∠ABC=24°.
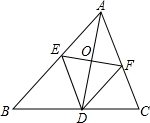 如图,△ABC的∠BAC的平分线AD被EF垂直平分,且E、F分别在AB,AC上,求证:四边形AEDF是菱形.
如图,△ABC的∠BAC的平分线AD被EF垂直平分,且E、F分别在AB,AC上,求证:四边形AEDF是菱形.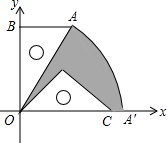 已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.
已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.