Question

2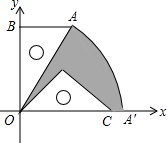．已知：如图，有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等，把该套三角板放置在平面直角坐标系中，且AB=3．
（1）若双曲线的一个分支恰好经过点A，求双曲线的解析式；
（2）若把含30°的直角三角板绕点O按顺时针方向旋转后，斜边OA恰好与x轴重叠，点A落在点A′，试求图中阴影部分的面积（结果保留π）．

Answer 1

分析 （1）在Rt△OBA中，由∠AOB=30°，AB=3利用特殊角的正切值即可求出OB的长度，从而得出点A的坐标，设双曲线的解析式为y=$\frac{k}{x}$（k≠0），利用待定系数法即可求出反比例函数解析式；
（2）在Rt△OBA中，利用勾股定理即可求出OA的长度，在等腰直角三角形ODC中，根据OC的长度可求出OD的长，结合图形即可得出阴影部分的面积为扇形AOA′的面积减去三角形ODC的面积，结合扇形与三角形的面积公式即可得出结论．

解答 解：（1）在Rt△OBA中，∠AOB=30°，AB=3，tan∠AOB=$\frac{AB}{OB}$，
∴OB=$\frac{AB}{tan∠AOB}$=$\frac{3}{tan30°}$=3$\sqrt{3}$，
∴A（3，3$\sqrt{3}$）．
设双曲线的解析式为y=$\frac{k}{x}$（k≠0），
∴3$\sqrt{3}$=$\frac{k}{3}$，k=9$\sqrt{3}$，
∴双曲线的解析式为y=$\frac{9\sqrt{3}}{x}$．
（2）在Rt△OBA中，AB=3，OB=3$\sqrt{3}$，∠ABO=90°，
∴OA=$\sqrt{A{B}^{2}+O{B}^{2}}$=6．
∵∠AOA′=90°-∠AOB=60°，
∴S_扇形AOA′=$\frac{60}{360}$πOA²=6π．
在Rt△OCD中，∠DOC=45°，OC=OB=3$\sqrt{3}$，
∴OD=OC•cos∠DOC=3$\sqrt{3}$×$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{6}}{2}$，
∴S_阴影=S_扇形AOA′-S_△DOC=6π-$\frac{1}{2}$OD²=6π-$\frac{27}{4}$．
答：图中阴影部分的面积为（6π-$\frac{27}{4}$）平方单位．

点评 本题考查了勾股定理、待定系数法求函数解析式、特殊角的三角函数值、扇形的面积以及等腰直角三角形的性质，解题的关键是：（1）求出点A的坐标；（2）利用分割图形求面积法求出阴影部分的面积．本题属于中档题，难度不大，解决该题型题目时，将不规则的图形的面积表示成多个规则图形的面积之和（差）的形式是关键．