题目内容
6．一个扇形的半径是3，圆心角是240°，这个扇形的弧长是（ ）| A． | 2π | B． | 4π | C． | 8π | D． | 12π |
分析 根据弧长公式l=$\frac{nπr}{180}$进行解答即可．
解答 解：根据弧长的公式l=$\frac{nπr}{180}$，
得到：$\frac{240π×3}{180}$=4π．
故选：B．
点评 本题考查了弧长的计算，熟记弧长公式即可解答该题．
练习册系列答案
相关题目
在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人距B地的距离y（km）与行驶时间x（h）之间的函数图象，根据图象解答以下问题：
17．为节能减排，郑州市政府鼓励居民节约用电，为了解居民用电情况，在某小区随机抽查了20户家庭的月用电量，结果如表：
则关于这20户家庭的月用电量，下列说法正确的是（ ）
| 月用电量（度） | 4 | 5 | 6 | 8 | 9 |
| 户数 | 2 | 5 | 7 | 4 | 1 |
| A． | 中位数是5度 | B． | 众数是6度 | C． | 平均数是6度 | D． | 极差是4度 |
14．在某校初三年级古诗词比赛中，初三（1）班60名学生的成绩统计如下：
则该班学生成绩的中位数和众数分别是（ ）
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 1 | 2 | 8 | 23 | 22 | 4 |
| A． | 80，80 | B． | 70，80 | C． | 80，90 | D． | 90，80 |
1．一枚质地均匀的正方体骰子的六个面上分别刻有1到6的点数，投掷此骰子，朝上面的点数为奇数的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
11．
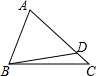如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（ ）
如图所示，点D是△ABC的边AC上一点（不含端点），AD=BD，则下列结论正确的是（ ）| A． | AC＞BC | B． | AC=BC | C． | ∠A＞∠ABC | D． | ∠A=∠ABC |
18．
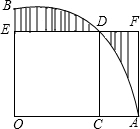如图，扇形AOB的圆心角为直角，正方形OCDE的顶点C，E，D分别在OA，OB，弧AB上，过点A作AF⊥ED，交ED的延长线于点F，已知图中阴影部分的面积为$\sqrt{2}$-1，则正方形OCDE边长为（ ）
如图，扇形AOB的圆心角为直角，正方形OCDE的顶点C，E，D分别在OA，OB，弧AB上，过点A作AF⊥ED，交ED的延长线于点F，已知图中阴影部分的面积为$\sqrt{2}$-1，则正方形OCDE边长为（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 3 |
15．
如图，在△ABC中，D、E、F分别是边AB、AC、BC上的点，连接EF，CD相交于点G，若四边形BDEF是平行四边形，则下列说法不正确的是（ ）
如图，在△ABC中，D、E、F分别是边AB、AC、BC上的点，连接EF，CD相交于点G，若四边形BDEF是平行四边形，则下列说法不正确的是（ ）| A． | $\frac{AD}{DB}$=$\frac{DG}{CG}$ | B． | $\frac{AD}{DB}$=$\frac{EG}{GF}$ | C． | $\frac{AD}{DB}$=$\frac{BF}{BC}$ | D． | $\frac{AD}{DB}$=$\frac{DE}{FC}$ |
如图，已知点C为反比例函数y=-$\frac{6}{x}$上一点，过点C向坐标轴引垂线，垂足分别为A，B，那么四边形AOBC的面积为（ ）