题目内容
16. 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人距B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:(1)写出A、B两地之间的距离;
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.
分析 (1)根据x=0时,甲距离B地30千米,由此即可解决问题.
(2)根据相遇时间=$\frac{距离}{速度和}$即可解决.
(3)分三个时间段求出时间即可,①是相遇前,则15x+30x=30-3,②是相遇后,则15x+30x=30+3,③若是甲到达B地前,而乙到达A地后按原路返回时,则15x-30(x-1)=3,分别解方程即可.
解答 解:(1)x=0时,甲距离B地30千米,
所以,A、B两地的距离为30千米;
(2)由图可知,甲的速度:30÷2=15千米/时,
乙的速度:30÷1=30千米/时,
30÷(15+30)=$\frac{2}{3}$,$\frac{2}{3}$×30=20千米,
所以,点M的坐标为($\frac{2}{3}$,20),表示甲、乙两人出发$\frac{2}{3}$小时后相遇,此时距离B地20千米;
(3)设x小时甲、乙两人相距3km,
①若是相遇前,则15x+30x=30-3,解得x=$\frac{3}{5}$,
②若是相遇后,则15x+30x=30+3,解得x=$\frac{11}{15}$,
③若是甲到达B地前,而乙到达A地后按原路返回时,
则15x-30(x-1)=3,
解得x=$\frac{9}{5}$,
所以,当$\frac{3}{5}$≤x≤$\frac{11}{5}$或$\frac{9}{5}$≤x≤2时,甲、乙两人能够用无线对讲机保持联系.
点评 本题考查一次函数的应用、相遇问题等知识,理解题意是解题的关键,考虑问题要全面,不能漏解,属于中考常考题型.

练习册系列答案
相关题目
6.(-3)×2的结果是( )
| A. | -5 | B. | -6 | C. | -1 | D. | 6 |
4.-3-(-4)的结果是( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
11.下列计算结果为a5的是( )
| A. | (a3)2 | B. | a3+a2 | C. | a6-a1 | D. | a3•a2 |
1.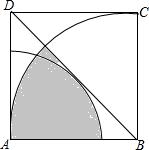 如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )
如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )
 如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )
如图所示,以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,以顶点B为圆心,正方形的边长为半径的弧,已知正方形的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | $\frac{π}{2}-1$ | C. | $\frac{5π}{4}-1$ | D. | $\frac{3π}{4}-1$ |
6.一个扇形的半径是3,圆心角是240°,这个扇形的弧长是( )
| A. | 2π | B. | 4π | C. | 8π | D. | 12π |
 如图,一束平行太阳光照射到等边三角形上,若∠α=28°,则∠β=32°.
如图,一束平行太阳光照射到等边三角形上,若∠α=28°,则∠β=32°. 如图,矩形ABCD中,点O在BC上,OB=2OC=2,以O为圆心OB的长半径画弧,这条弧恰好经过点D,则图中阴影部分的面积为$\frac{2π}{3}$-$\sqrt{3}$.
如图,矩形ABCD中,点O在BC上,OB=2OC=2,以O为圆心OB的长半径画弧,这条弧恰好经过点D,则图中阴影部分的面积为$\frac{2π}{3}$-$\sqrt{3}$. 如图,随机地闭合开关S1,S2,S3,S4,S5中的三个,能够使灯泡L1,L2同时发光的概率是$\frac{1}{5}$.
如图,随机地闭合开关S1,S2,S3,S4,S5中的三个,能够使灯泡L1,L2同时发光的概率是$\frac{1}{5}$.