题目内容

18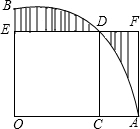．如图，扇形AOB的圆心角为直角，正方形OCDE的顶点C，E，D分别在OA，OB，弧AB上，过点A作AF⊥ED，交ED的延长线于点F，已知图中阴影部分的面积为$\sqrt{2}$-1，则正方形OCDE边长为（　　）
A．1B．$\sqrt{2}$C．2D．3

分析 通过观察图形可知DE=DC，BE=AC，$\widehat{BD}$=$\widehat{AD}$，则阴影部分的面积正好等于长方形ACDF的面积，于是列方程即可得到结论．

解答 解：连接OD，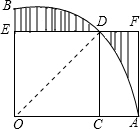

设正方形OCDE的边长为a，
∴OD=$\sqrt{2}$a，
∴AC=$\sqrt{2}$a-a，
∵DE=DC，BE=AC，$\widehat{BD}$=$\widehat{AD}$，
∴S阴影=长方形ACDF的面积=AC•CD=（$\sqrt{2}$a-a）•a=$\sqrt{2}$-1，
∴a=1，
故选A．

点评 本题考查了扇形的面积计算及等积变换的知识，关键是要把不规则的图形通过几何变换转化为规则图形的面积求解．

练习册系列答案
相关题目
8．如图，矩形ABCD中，点O在BC上，OB=2OC=2，以O为圆心OB的长半径画弧，这条弧恰好经过点D，则图中阴影部分的面积为$\frac{2π}{3}$-$\sqrt{3}$．
9．|-2|=（　　）
A．2B．-2C．±2D．$\frac{1}{2}$
6．一个扇形的半径是3，圆心角是240°，这个扇形的弧长是（　　）
A．2πB．4πC．8πD．12π
13．尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．
求证：a2+b2=5c2
该同学仔细分析后，得到如下解题思路：
先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故$\frac{EP}{BP}=\frac{PF}{PA}=\frac{EF}{BA}=\frac{1}{2}$，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证
（1）请你根据以上解题思路帮尤秀同学写出证明过程．
（2）利用题中的结论，解答下列问题：
在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求MG2+MH2的值．
3．下列函数：
①y=$\frac{1}{2}$x；②y=2-x；③y=$\frac{2}{x}$（x＞0）；④y=x2，
其中y的值随x值得增大而增大的有（　　）
A．4个B．3个C．2个D．1个
10．如图所示得到几何体是由一个圆柱体和一个长方形组成的，则这个几何体的左视图是（　　）
A．B．C．D．
7．下列等式一定成立的是（　　）
A．2a2-3a2=-a2B．（a+2）2=a2+4C．a6÷a3=a2D．（a+3）（a-3）=a2-3
8．抛物线y=ax2+bx+4A（1，-1），B（5，-1），与y轴交于点C．
（1）求抛物线的函数表达式；
（2）如图1，连接CB，若点P在直线BC上方的抛物线上，△BCP的面积为15，求点P的坐标；
（3）如图2，⊙O1过点A、B、C三点，AE为直径，点M为弧ACE上的一动点（不与点A，E重合），∠MBN为直角，边BN与ME的延长线交于N，求线段BN长度的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网