题目内容

1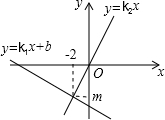．同一平面直角坐标系中，一次函数y=k1x+b的图象与正比例函数y=k2x的图象如图所示，则关于x的方程k1x-2b＞k2x的解为（　　）
A．x＞-2B．x＜-2C．x＜2D．x＜4

分析 认真分析比较y=k1x+b与y=k1x-2b之间的联系可以发现，y=k1x-2b是由y=k1x+b向上平移-3b个单位得到的，据此得到两条直线交点的横坐标，进而得解．

解答 解：y=k1x-2b=k1x+b-3b是由y=k1x+b向上平移-3b个单位得到的，
∵y=k1x+b与y=k2x交点的横坐标为-2，
∴y=k1x-2b与y=k2x的交点的横坐标为4，
∴方程k1x-2b＞k2x的解为：x＜4．
故选：D．

点评 本题主要考查了利用一次函数解一元一次不等式的问题，找出不等式与一次函数之间的联系是解题的关键，要注意认真总结．

练习册系列答案
相关题目
11．解方程：$\frac{1-x}{x-2}$-$\frac{3}{2-x}$=1．
12．在?ABCD中，AB=3，BC=4，当?ABCD的面积最大时，下列结论：
①AC=5；②∠A+∠C=180°；③AC⊥BD；④AC=BD．
其中正确的有①②④．（填序号）
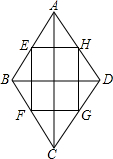9．如图，E、F、G、H分别是菱形ABCD四边的中点，菱形ABCD的面积为4$\sqrt{3}$cm2，对角线AC=2$\sqrt{2}$cm．
（1）求菱形ABCD对角线BD的长；
（2）求四边形EFGH的面积．
16．如图，在△ABC中，D，E是BC的三等分点，BC=15cm，AD=13cm，AE=12cm，F，G分别是AB，AC的中点，求四边形DEGF的周长和面积．
6．将抛物线C1：y=-x2-2x，绕着点M（1，0）旋转180°后，所得到的新抛物线C2的解析式是y=（x-3）2-1．
13．解方程（方程组）
（1）3x-7（x-1）=3-2（x+3）
（2）y-$\frac{y-1}{2}$=2-$\frac{y+2}{6}$．
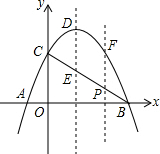10．已知抛物线y=-x2+bx+c与x轴相交于A、B两点，与y轴相交于点C，且顶点为D（1，4）．
（1）求b和c的值；
（2）如图，连接BC，与抛物线的对称轴相交于点E，点P是线段BC上一动点，作点P作PF∥DF，交抛物线于点F，设点P的横坐标为m；
①用含m的代数式表示线段PF的长，并求当四边形DEPF为平行四边形时m的值；
②设△BCF的面积为S，求S与m的函数关系式，并求出s的最大值．
11．已知x为实数，求代数式$\sqrt{x-4}$+$\sqrt{4-x}$-$\sqrt{2x}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网