题目内容
16.二次函数y=-x2+3x图象的对称轴是直线x=$\frac{3}{2}$.分析 把二次函数解析式化为顶点式可求得答案.
解答 解:
∵y=-x2+3x=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
∴抛物线对称轴为直线x=$\frac{3}{2}$,
故答案为:直线x=$\frac{3}{2}$.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,对称轴为x=h,顶点坐标为(h,k).

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
8.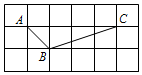 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )
 如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )
如图,方格纸中的每个小方格都是边长为1的正方形,△ABC的顶点都在格点上,则sin∠ACB的值为( )| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{10}}{10}$ | D. | $\frac{3\sqrt{10}}{10}$ |
5.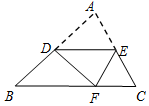 如图,D是AB的中点,将△ABC沿过点D的直线折叠,使点A落在BC边上点F处,若∠B=50°,则∠EDF的度数为( )
如图,D是AB的中点,将△ABC沿过点D的直线折叠,使点A落在BC边上点F处,若∠B=50°,则∠EDF的度数为( )
 如图,D是AB的中点,将△ABC沿过点D的直线折叠,使点A落在BC边上点F处,若∠B=50°,则∠EDF的度数为( )
如图,D是AB的中点,将△ABC沿过点D的直线折叠,使点A落在BC边上点F处,若∠B=50°,则∠EDF的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 80° |
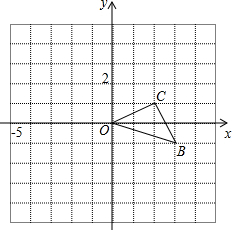 如图,已知O是坐标原点,以O点为位似中心在y轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),则B(3,-1)的对称点的坐标为(-6,2).
如图,已知O是坐标原点,以O点为位似中心在y轴的左侧将△OBC放大两倍(即新图与原图的相似比为2),则B(3,-1)的对称点的坐标为(-6,2). 如图,△ABC中,AC=AB,S△ABC=30,且底边长为10,求出这个等腰三角形的腰长.
如图,△ABC中,AC=AB,S△ABC=30,且底边长为10,求出这个等腰三角形的腰长. 如图,是一副扑克牌中取出的两组牌,分别是红桃1,2,3和方块1,2,3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张.
如图,是一副扑克牌中取出的两组牌,分别是红桃1,2,3和方块1,2,3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张.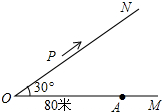 如图,∠MON=30°,在距离O点80米的A处有一所学校,当重型运输卡车P沿道路ON方向行驶时,距离卡车50米范围内都会受到卡车噪声的影响.
如图,∠MON=30°,在距离O点80米的A处有一所学校,当重型运输卡车P沿道路ON方向行驶时,距离卡车50米范围内都会受到卡车噪声的影响.