题目内容
1.阅读下列材料:因为$\frac{1}{1×3}$=$\frac{1}{2}×(1-\frac{1}{3})$,
$\frac{1}{3×5}$=$\frac{1}{2}×(\frac{1}{3}-\frac{1}{5})$,
$\frac{1}{5×7}$=$\frac{1}{2}×(\frac{1}{5}-\frac{1}{7})$,
$\frac{1}{2013×2015}$=$\frac{1}{2}×(\frac{1}{2013}-\frac{1}{2015})$,…
所以$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2013×2015}$=$\frac{1}{2}×(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2013}-\frac{1}{2015})$.
解答下列问题:
(1)在和式$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…中,第五项为$\frac{1}{9×11}$,第n项为$\frac{1}{(2n-1)(2n+1)}$.
(2)利用上述结论计算:
$\frac{1}{x(x+2)}$+$\frac{1}{(x+2)(x+4)}$+$\frac{1}{(x+4)(x+6)}$+…+$\frac{1}{(x+2014)(x+2016)}$.
分析 (1)由已知等式得出第n项为$\frac{1}{(2n-1)(2n+1)}$,据此可得;
(2)利用裂项法得出原式=$\frac{1}{2}$×($\frac{1}{x}$-$\frac{1}{x+2}$)+$\frac{1}{2}$×($\frac{1}{x+2}$-$\frac{1}{x+4}$)+$\frac{1}{2}$×($\frac{1}{x+4}$-$\frac{1}{x+6}$)+…+$\frac{1}{2}$×($\frac{1}{x+2014}$-$\frac{1}{x+2016}$),进一步运算可得.
解答 解:(1)∵第1项$\frac{1}{1×3}$=$\frac{1}{(2×1-1)(2×1+1)}$,
第2项$\frac{1}{3×5}$=$\frac{1}{(2×2-1)(2×2+1)}$,
第3项$\frac{1}{5×7}$=$\frac{1}{(2×3-1)(2×3+1)}$,
∴第5项为$\frac{1}{(2×5-1)(2×5+1)}$=$\frac{1}{9×11}$,
第n项为$\frac{1}{(2n-1)(2n+1)}$,
故答案为:$\frac{1}{9×11}$,$\frac{1}{(2n-1)(2n+1)}$;
(2)原式=$\frac{1}{2}$×($\frac{1}{x}$-$\frac{1}{x+2}$)+$\frac{1}{2}$×($\frac{1}{x+2}$-$\frac{1}{x+4}$)+$\frac{1}{2}$×($\frac{1}{x+4}$-$\frac{1}{x+6}$)+…+$\frac{1}{2}$×($\frac{1}{x+2014}$-$\frac{1}{x+2016}$)
=$\frac{1}{2}$×($\frac{1}{x}$-$\frac{1}{x+2}$+$\frac{1}{x+2}$-$\frac{1}{x+4}$+$\frac{1}{x+4}$-$\frac{1}{x+6}$+…+$\frac{1}{x+2014}$-$\frac{1}{x+2016}$)
=$\frac{1}{2}$×($\frac{1}{x}$-$\frac{1}{x+2016}$)
=$\frac{1}{2}$×$\frac{x+2016-x}{x(x+2016)}$
=$\frac{1008}{x(x+2016)}$.
点评 本题主要考查数字的变化规律和分式的化简,根据题意得出第n项为$\frac{1}{(2n-1)(2n+1)}$且$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)是解题的关键.

| A. | 15×103 | B. | 1.5×104 | C. | 1.5×103 | D. | 0.15×105 |
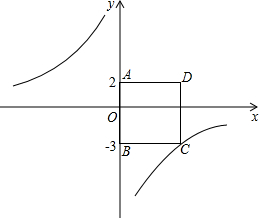 如图,在平面直角坐标系中,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=$\frac{k}{x}$的图象经过点C.
如图,在平面直角坐标系中,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y=$\frac{k}{x}$的图象经过点C.