题目内容
15.已知$\left\{\begin{array}{l}x=2\\ y=-3\end{array}$是关于x,y的二元一次方程3x=y+a的解,求a(a-1)的值.分析 根据$\left\{\begin{array}{l}x=2\\ y=-3\end{array}$是关于x,y的二元一次方程3x=y+a的解,可以求得a的值,然后代入a(a-1)即可解答本题.
解答 解:∵$\left\{\begin{array}{l}x=2\\ y=-3\end{array}$是关于x,y的二元一次方程3x=y+a的解,
∴3×2=-3+a,
解得,a=9,
∴a(a-1)=9×(9-1)=72,
即a(a-1)的值是72.
点评 本题考查二元一次方程的解,解答本题的关键是明确二元一次方程的解的意义.

练习册系列答案
相关题目
20. 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )
 如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )
如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形,要求等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上,则剪下的等腰三角形一腰上的高不可能是( )| A. | 4 | B. | $\sqrt{15}$ | C. | $\sqrt{7}$ | D. | $\sqrt{6}$ |
4.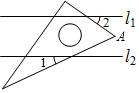 已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )
已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )
 已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )
已知,直线l1∥l2,一块含30°角的直角三角尺如图放置,∠1=25°,则∠2等于( )| A. | 45° | B. | 40° | C. | 35° | D. | 30° |
5.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{{a}^{2}+{b}^{2}}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{25a}$ | D. | $\sqrt{4a+4}$ |
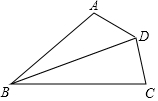 如图,在四边形ABCD中,已知BD平分∠ABC,∠A+∠C=180°,试说明AD=CD的理由.
如图,在四边形ABCD中,已知BD平分∠ABC,∠A+∠C=180°,试说明AD=CD的理由.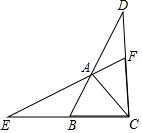 如图,△ABC是等边三角形,延长BA到点D,延长CB到点E,使BE=AD,连接CD,AE.
如图,△ABC是等边三角形,延长BA到点D,延长CB到点E,使BE=AD,连接CD,AE.