题目内容
3.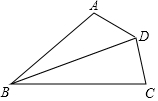 如图,在四边形ABCD中,已知BD平分∠ABC,∠A+∠C=180°,试说明AD=CD的理由.
如图,在四边形ABCD中,已知BD平分∠ABC,∠A+∠C=180°,试说明AD=CD的理由.
分析 过点D作DE⊥AB交BA的延长线于E,作DF⊥BC于F,根据角平分线上的点到角的两边距离相等可得DE=DF,再求出∠ADE=∠CDF,然后利用“角角边”证明△ADE和△CDF全等,根据全等三角形对应边相等证明即可.
解答 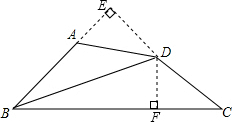 证明:如图,过点D作DE⊥AB交BA的延长线于E,作DF⊥BC于F,
证明:如图,过点D作DE⊥AB交BA的延长线于E,作DF⊥BC于F,
所以,∠EDF+∠BAD=180°,
∵BD平分∠ABC,
∴DE=DF,
∵∠BAD与∠BCD互补,
∴∠ADE=∠CDF,
在△ADE和△CDF中,
$\left\{\begin{array}{l}{∠ADE=∠CDF}\\{∠E=∠CFD=90°}\\{DE=DF}\end{array}\right.$,
∴△ADE≌△CDF(AAS),
∴AD=CD.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
11.若x=-3是方程kx-x+6=0的解,则k的值是( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
18. 如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
 如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )| A. | 大于90° | B. | 等于90° | C. | 小于90° | D. | 无法确定 |
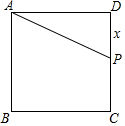 如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围. 把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=35°,则下面五个结论:①∠CEF=35°;②∠AEC=145°;③∠BGE=70°;④∠EFD′=110°;⑤∠D′FD=70°.其中正确的是①③⑤.(只填序号)
把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=35°,则下面五个结论:①∠CEF=35°;②∠AEC=145°;③∠BGE=70°;④∠EFD′=110°;⑤∠D′FD=70°.其中正确的是①③⑤.(只填序号)