题目内容
10.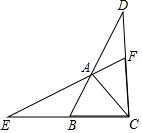 如图,△ABC是等边三角形,延长BA到点D,延长CB到点E,使BE=AD,连接CD,AE.
如图,△ABC是等边三角形,延长BA到点D,延长CB到点E,使BE=AD,连接CD,AE.(1)求证:AE=CD;
(2)若延长EA交CD于点F,求∠CFE的度数.
分析 (1)根据等边三角形的性质得到AB=AC,∠CAB=∠ABC=60°,根据全等三角形的性质即可得到结论;
(2)根据全等三角形的性质得到∠E=∠D,∠EAB=∠ACD=∠DAF,根据三角形的内角和和三角形的外角的性质得到2∠EAF+60°=180°,于是得到结论.
解答 (1)证明:∵△ABC是等边三角形,
∴AB=AC,∠CAB=∠ABC=60°,
∴∠DAC=∠ABE=120°,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABE=∠CAD}\\{BE=AD}\end{array}\right.$,
∴△ABE≌△ACD,
∴AE=CD;
(2)∵△ABE≌△ACD,
∴∠E=∠D,∠EAB=∠ACD=∠DAF,
∵∠CFE=∠D+∠DAF=∠E+∠ACF,∵∠EFC+∠E+∠ACB+∠ACF=180°,
∴2∠EAF+60°=180°,
∴∠CFE=60°.
点评 本题考查等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识,属于基础题,中考常考题型.

练习册系列答案
相关题目
4.不等式组$\left\{\begin{array}{l}{x-a≥0}\\{x-a≤1}\end{array}\right.$的解集中任何x的值均在2≤x≤5的范围内,则a的取值范围是( )
| A. | a≥2 | B. | 2≤a≤4 | C. | a≤4 | D. | a≥2且a≠4 |
18. 如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
 如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )
如图,在△ABC中,以AC为边的正方形I的面积为28,以BC为边的正方形Ⅱ的面积为36,若AB=8,则∠ACB的度数( )| A. | 大于90° | B. | 等于90° | C. | 小于90° | D. | 无法确定 |
 如图,∠ABC=∠BCD
如图,∠ABC=∠BCD 如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.求证:
如图,△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.求证: 如图,直线AC∥BD,P在直线AB上(不与点A,B重合).
如图,直线AC∥BD,P在直线AB上(不与点A,B重合).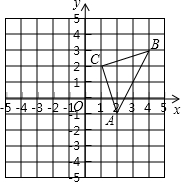 如图所示,△ABC的顶点都在平面直角坐标系的网格上.
如图所示,△ABC的顶点都在平面直角坐标系的网格上.