题目内容
19.从3,0,-1,-2,-3这五个数中抽取一个数,作为函数y=(m+2)x和关于x的一元二次方程x2+x+m+1=0中m的值,若恰好使函数的图象经过第一、三象限,且使方程有实数根,则满足条件的m的值是-1.分析 确定使函数的图象经过第一、三象限的m的值,然后确定使方程有实数根的m值,找到同时满足两个条件的m的值即可.
解答 解:∵函数y=(m+2)x的图象经过第一、三象限,
∴m+2>0,
解得:m>-2,
∵方程x2+x+m+1=0有实数根,
∴△=1-4(m+1)≥0,
解得:m≤-$\frac{3}{4}$,
综上,m的取值范围是-2<m≤-$\frac{3}{4}$,
在3,0,-1,-2,-3中符合该范围的m的值是-1,
故答案为:-1.
点评 本题考查了一次函数图象与系数的关系及根的判别式的知识,根据一次函数性质与方程的根的判别式得出m的取值范围是解答此题的关键.

练习册系列答案
相关题目
4.已知抛物线y=-(x-m)2的顶点为A,直线l:y=$\sqrt{3}$x-$\sqrt{3}$m,其中m>0
(1)求抛物线的对称轴及点A的坐标(用含m的代数式表示);
(2)证明:点A在直线l上.
(1)求抛物线的对称轴及点A的坐标(用含m的代数式表示);
(2)证明:点A在直线l上.
14.下列调查中,适合采用普查的是( )
| A. | 调查全国中学生心理健康现状 | |
| B. | 调查我市食品合格情况 | |
| C. | 调查你所在的班级同学的身高情况 | |
| D. | 调查桂林电视台某电视节目的收视率 |
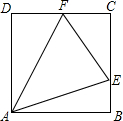 如图,已知正方形ABCD的边长为1,点E,F分别在边BC,CD上,且∠EAF=45°,则△CEF的周长为2.
如图,已知正方形ABCD的边长为1,点E,F分别在边BC,CD上,且∠EAF=45°,则△CEF的周长为2. 如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.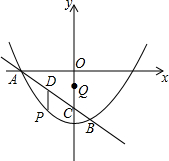 如图,已知抛物线y=ax2+c与直线$y=-\frac{3}{4}x-3$交于A,B两点,直线AB与y轴交于点C,点B的坐标为(1,$-\frac{15}{4}$),动点P在直线AB下方的抛物线上,动点Q在y轴上,动点D在线段AB上,且PD∥y轴.
如图,已知抛物线y=ax2+c与直线$y=-\frac{3}{4}x-3$交于A,B两点,直线AB与y轴交于点C,点B的坐标为(1,$-\frac{15}{4}$),动点P在直线AB下方的抛物线上,动点Q在y轴上,动点D在线段AB上,且PD∥y轴.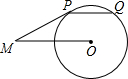 如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )
如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )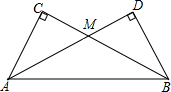 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.