题目内容
18.已知x2+(a+3)x+a+1=0是关于x的一元二次方程.(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1,x2,且x12+x22=10,求实数a的值.
分析 (1)先计算判别式,再进行配方得到△=(a+1)2+4,然后根据非负数的性质得到△>0,再利用判别式的意义即可得到方程总有两个不相等的实数根;
(2)根据根与系数的关系得到x1+x2=-(a+3),x1x2=a+1,再利用完全平方公式由x12+x22=10得(x1+x2)2-2x1x2=10,则(a+3)2-2(a+1)=10,然后解关于a的方程即可.
解答 (1)证明:△=(a+3)2-4(a+1)
=a2+6a+9-4a-4
=a2+2a+5
=(a+1)2+4,
∵(a+1)2≥0,
∴(a+1)2+4>0,即△>0,
∴方程总有两个不相等的实数根;
(2)解:根据题意得x1+x2=-(a+3),x1x2=a+1,
∵x12+x22=10,
∴(x1+x2)2-2x1x2=10,
∴(a+3)2-2(a+1)=10,
整理得a2+4a-3=0,解得a1=-2+$\sqrt{7}$,a2=-2-$\sqrt{7}$,
即a的值为-2+$\sqrt{7}$或-2-$\sqrt{7}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
相关题目
13.在平面直角坐标系中,将点P(a,b)关于原点对称得到点P1,再将点P1向左平移2个单位长度得到点P2,则点P2的坐标是( )
| A. | (b-2,-a) | B. | (b+2,-a) | C. | (-a+2,-b) | D. | (-a-2,-b) |
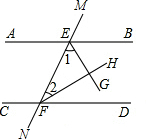 如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?
如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?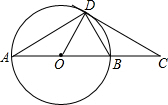 如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,DC与AB的延长线交于点C,∠A=30°,给出下面3个结论:∠BDC=∠A;AB=2BC;AD2=3BC2;其中正确结论的个数是( )
如图,AB是⊙O的直径,CD是⊙O的切线,切点为D,DC与AB的延长线交于点C,∠A=30°,给出下面3个结论:∠BDC=∠A;AB=2BC;AD2=3BC2;其中正确结论的个数是( )