题目内容
5.函数y=$\frac{{k}^{2}+1}{x}$(k为常数)的图象过点(-2,y1)和(-$\sqrt{5}$,y2),则y1,y2的大小关系是(填“>”,“=”,“<”)y1<y2.分析 把两个点的坐标分别代入反比例函数解析式,计算出y1和y2的值,然后比较大小即可.
解答 解:∵函数y=$\frac{{k}^{2}+1}{x}$(k为常数)的图象过点(-2,y1)和(-$\sqrt{5}$,y2),
∴y1=-$\frac{{k}^{2}+1}{2}$,y2=-$\frac{{k}^{2}+1}{\sqrt{5}}$,
∴y1<y2.
故答案为y1<y2.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
16.已知点P(x1,-2)、Q(x2,2)、R(x3,3)三点都在反比例函数y=$\frac{{a}^{2}+1}{x}$的图象上,则下列关系正确的是( )
| A. | x1<x3<x2 | B. | x<1x2<x3 | C. | x3<x2<x1 | D. | x2<x3<x1 |
13.若$\sqrt{a}$是二次根式,则( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
20.若函数y=$\frac{k}{x}$(k≠0)的图象过点($\frac{1}{2}$,$\frac{4}{3}$),则此函数图象位于( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
10.下列根式中可以与$\sqrt{5}$合并的是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{20}$ | D. | $\sqrt{25}$ |
14. 如图,有三张卡片,它们背面完全相同,现将这三张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,放回后再从中随机抽取一张,以去正面的数字作为b的值,则点(a,b)在第三象限的概率是( )
如图,有三张卡片,它们背面完全相同,现将这三张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,放回后再从中随机抽取一张,以去正面的数字作为b的值,则点(a,b)在第三象限的概率是( )
 如图,有三张卡片,它们背面完全相同,现将这三张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,放回后再从中随机抽取一张,以去正面的数字作为b的值,则点(a,b)在第三象限的概率是( )
如图,有三张卡片,它们背面完全相同,现将这三张卡片背面朝上洗均匀后随机抽取一张,以其正面的数字作为a的值,放回后再从中随机抽取一张,以去正面的数字作为b的值,则点(a,b)在第三象限的概率是( )| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图,已知线段AB,分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,连接AC,BC,BD,CD.其中AB=4,CD=5,则四边形ABCD的面积为10.
如图,已知线段AB,分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,连接AC,BC,BD,CD.其中AB=4,CD=5,则四边形ABCD的面积为10.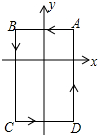 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,当a=12时,小聪聪一眼就看出细线另一端所在位置的点的坐标是(-1,1),那么当a=2015时,细线另一端所在位置的点的坐标是(-1,-2).
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上,当a=12时,小聪聪一眼就看出细线另一端所在位置的点的坐标是(-1,1),那么当a=2015时,细线另一端所在位置的点的坐标是(-1,-2).