题目内容
20．若函数y=$\frac{k}{x}$（k≠0）的图象过点（$\frac{1}{2}$，$\frac{4}{3}$），则此函数图象位于（ ）| A． | 第一、二象限 | B． | 第一、三象限 | C． | 第二、三象限 | D． | 第二、四象限 |
分析 根据反比例函数图象上点的坐标特征求出k的值，然后根据反比例函数的性质判断图象的位置．
解答 解：根据题意得k=$\frac{1}{2}$×$\frac{4}{3}$=$\frac{2}{3}$＞0，
所以反比例函数得图象分布在第一、三象限．
故选B．
点评 本题考查了反比例函数图象上点的坐标特征：反比例函数y=$\frac{k}{x}$（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．
练习册系列答案
名校课堂系列答案
相关题目
11．
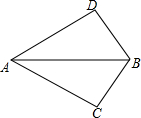如图所示，已知∠ABD=∠ABC，补充一个条件，可使△ABD≌△ABC，那么补充的条件不能是（ ）
如图所示，已知∠ABD=∠ABC，补充一个条件，可使△ABD≌△ABC，那么补充的条件不能是（ ）| A． | AD=AC | B． | BD=CB | C． | ∠D=∠C | D． | ∠DAB=∠CAB |
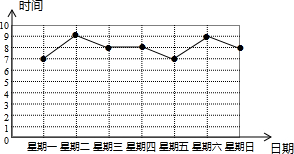为了在中考时保持充沛的精力，在中考前一周要保证充足的睡眠，小明的妈妈为他记录了七天的睡眠时间，绘制了如下折线统计图，根据统计图请计算小明一周内平均每天的睡眠时间是（ ）
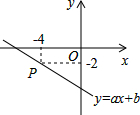在教学活动中我们知道，任何一个二元一次方程的图象都是一条直线，如图，已知直线y=ax-6过点P（-4，-2），则关于x、y的方程组$\left\{\begin{array}{l}{y=ax-6}\\{y=\frac{1}{2}x}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-4}\\{y=-2}\end{array}\right.$．