题目内容
20.直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图1,分别过点A和B作AD⊥直线l于点D,BE⊥直线l于点E.△ACD与△CBE是否全等,并说明理由;
(2)当AC=8cm,BC=6cm时,如图2,点B与点F关于直线l对称,连接BF、CF(BF⊥直线l,BC=CF).点M是AC上一点,点N是CF上一点,分别过点M、N作MD⊥直线l于点D,NE⊥直线l于点E.点M从A点出发,以每秒1cm的速度沿A→C路径运动,终点 为C.点N从F点出发,以每秒3cm的速度沿F→C→B→C→F路径运动,终点为F.点M、N同时开始运动,各自达到相应的终点时停止运动.设运动时间为t秒,请求出所有使△MDC与△CEN全等的t的值.
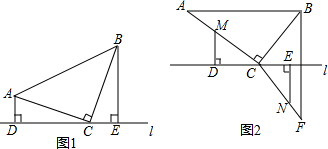
分析 (1)根据同角的余角相等得到∠DAC=∠ECB,根据全等三角形的判定定理证明即可;
(2)分点N沿F→C路径运动、点N沿C→B路径运动、点N沿B→C路径运动、点N沿C→F路径运动四种情况计算即可.
解答 解:(1)△ACD≌△CBE,
理由如下:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥直线l,
∴∠ACD+∠DAC=90°,
∴∠DAC=∠ECB,
在△ACD和△CBE中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠CEB}\\{CA=CB}\end{array}\right.$,
∴△ACD≌△CBE;
(2)由题意得,CF=BC=6cm,
由(1)得,∠DAC=∠ECB,∠ADC=∠CEB,
∴当CM=CN时,△MDC≌△CEN,
当点N沿F→C路径运动时,8-t=6-3t,
解得,t=-1,不合题意,
当点N沿C→B路径运动时,8-t=3t-6,
解得,t=3.5,
当点N沿B→C路径运动时,8-t=3t-12,
解得,t=5,
当点N沿C→F路径运动时,8-t=3t-18,
解得,t=6.5,
综上所述,当t=3.5秒或5秒或6.5秒时,△MDC≌△CEN.
点评 本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.

练习册系列答案
相关题目
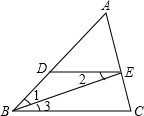 已和,如图,BE平分∠ABC,∠1=∠2,请说明∠AED=∠C.根据提示填空.
已和,如图,BE平分∠ABC,∠1=∠2,请说明∠AED=∠C.根据提示填空.