题目内容
5.若5+$\sqrt{10}$的整数部分为a,小数部分为b,则a=8,b=$\sqrt{10}$-3.分析 先估算$\sqrt{10}$的范围,再求出5+$\sqrt{10}$的范围,即可得出答案.
解答 解:∵3<$\sqrt{10}$<4,
∴8<5+$\sqrt{10}$<9,
∴a=8,b=5+$\sqrt{10}$-8=$\sqrt{10}$-3,
故答案为:8,$\sqrt{10}$-3.
点评 本题考查了估算无理数的大小的应用,能正确估算$\sqrt{10}$的范围是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.-$\frac{1}{8}$的立方根是( )
| A. | -$\frac{1}{2}$ | B. | $±\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
20.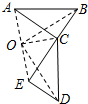 如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
 如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )| A. | AB⊥CD | B. | AC⊥CE | ||
| C. | BC⊥DE | D. | 点C与点C是两个三角形的对应点 |
10.15的负的平方根介于( )
| A. | -4与-3之间 | B. | -5与-4之间 | C. | -3与-2之间 | D. | -2与-1之间 |
17.在多项式3x2y3z+4x5y2+6x4yz2中,各项的公因式是( )
| A. | x2yz | B. | 12x5y3z2 | C. | 12x2yz | D. | x2y |
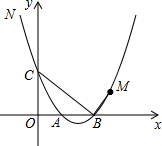 如图,抛物线y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3与y轴交于点C,与x轴交于点A、B(A在B左侧),点M(4,m)在抛物线上,且在对称轴右侧,点N在抛物线上,△BMN是以BM为直角边的直角三角形,求N点坐标.
如图,抛物线y=$\frac{1}{2}$x2$-\frac{5}{2}$x+3与y轴交于点C,与x轴交于点A、B(A在B左侧),点M(4,m)在抛物线上,且在对称轴右侧,点N在抛物线上,△BMN是以BM为直角边的直角三角形,求N点坐标.