题目内容
16.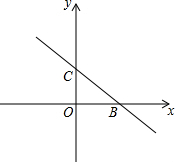 如图,已知直线y=-$\frac{2}{3}$x+2与x轴、y轴分别相交于点B、点C
如图,已知直线y=-$\frac{2}{3}$x+2与x轴、y轴分别相交于点B、点C(1)B、C两点的坐标分别为(3,0)、(0,2)
(2)若反比例函数y=$\frac{k}{x}$的图象经过线段BC的中点,则k的值为多少
(3)设Q为x轴上一点,在(2)中反比例函数的图象上是否存在这样一点M,使得以B、C、Q、M为顶点的四边形是平行四边形?若存在,求出点Q的坐标;若不存在,请说明理由.
分析 (1)先令y=0求出x的值,再令x=0求出y的值即可得出B、C两点的坐标;
(2)根据中点坐标公式求出BC的中点,代入反比例函数的解析式即可得出k的值;
(3)设Q(a,0),M(x,$\frac{3}{2x}$),再分BC、CM分别为平行四边形的对角线两种情况进行讨论.
解答 解:(1)∵令y=0,则x=3;令x=0,则y=2,
∴B(3,0),C(0,2).
故答案为:(3,0),(0,2);
(2)∵B(3,0),C(0,2),
∴线段BC的中点坐标为($\frac{3}{2}$,1).
∵反比例函数y=$\frac{k}{x}$的图象经过线段BC的中点,
∴k=$\frac{3}{2}$×1=$\frac{3}{2}$;
(3)存在.
∵由(2)知k=$\frac{3}{2}$,
∴反比例函数的解析式为y=$\frac{3}{2x}$,
设Q(a,0),M(x,$\frac{3}{2x}$).
如图所示,当BC为平行四边形的对角线时,$\frac{3}{2}$=$\frac{a+x}{2}$,1=$\frac{\frac{3}{2x}}{2}$,
解得a=$\frac{9}{4}$,x=$\frac{3}{4}$,
∴Q1($\frac{9}{4}$,0);
当CM为对角线时,$\frac{x}{2}$=$\frac{a+3}{2}$,$\frac{2+\frac{3}{2x}}{2}$=0,解得a=-$\frac{15}{4}$,
∴Q2(-$\frac{15}{4}$,0).
当BC和QM是平行四边形的边时,M的纵坐标是2,
把y=2代入y=$\frac{3}{2x}$得x=$\frac{3}{4}$.即CM=$\frac{3}{4}$,
则Q的横坐标是3+$\frac{3}{4}$=$\frac{15}{4}$,则Q3坐标是($\frac{15}{4}$,0)
综上所述,Q点的坐标为Q1($\frac{9}{4}$,0),Q2(-$\frac{15}{4}$,0),Q3($\frac{15}{4}$,0).
点评 本题考查的是反比例函数综合题,涉及到平行四边形的判定与性质等知识,在解答(3)时要注意进行分类讨论.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | $\sqrt{0.36}$与$\sqrt{3.6}$ | B. | $\sqrt{xy}$与$\sqrt{x+y}$ | C. | $\sqrt{5{x}^{2}y}$与$\sqrt{5x{y}^{2}}$ | D. | $\sqrt{x-y}$与$\sqrt{\frac{{x}^{2}-{y}^{2}}{x+y}}$ |
 如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.
如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.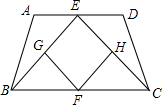 如图,等腰梯形ABCD,AD∥BC,AB=CD,E,F分别是AD,BC的中点,G,H分别是EB,EC的中点,求证:四边形EGFH是菱形.
如图,等腰梯形ABCD,AD∥BC,AB=CD,E,F分别是AD,BC的中点,G,H分别是EB,EC的中点,求证:四边形EGFH是菱形. 如图,在正方形ABCD和正方形CEFG中,点D在CG边上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,若H是AF的中点,则CH的长为$\sqrt{10}$.
如图,在正方形ABCD和正方形CEFG中,点D在CG边上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,若H是AF的中点,则CH的长为$\sqrt{10}$.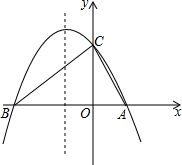 如图,抛物线与x轴交于A(2,0)、B两点,与y轴的交点为C(0,3),它的对称轴是直线x=-$\frac{1}{2}$
如图,抛物线与x轴交于A(2,0)、B两点,与y轴的交点为C(0,3),它的对称轴是直线x=-$\frac{1}{2}$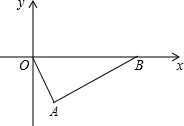 如图所示,在Rt△OAB中.斜边OB在x轴的正半轴上,直角顶点A在第四象限内,S△OAB=20,OA:AB=1:2,求A、B两点的坐标.
如图所示,在Rt△OAB中.斜边OB在x轴的正半轴上,直角顶点A在第四象限内,S△OAB=20,OA:AB=1:2,求A、B两点的坐标.