题目内容
4.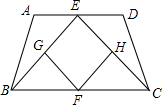 如图,等腰梯形ABCD,AD∥BC,AB=CD,E,F分别是AD,BC的中点,G,H分别是EB,EC的中点,求证:四边形EGFH是菱形.
如图,等腰梯形ABCD,AD∥BC,AB=CD,E,F分别是AD,BC的中点,G,H分别是EB,EC的中点,求证:四边形EGFH是菱形.
分析 先证明△AEB≌△DEC,从而得到BE=EC,然后由三角形中位线的性质证明EG=GF=FH=EH,从而证明四边形EGFH是菱形.
解答 解:∵四边形ABCD为等腰梯形,
∴∠A=∠D,AB=DC.
∵E是AD的中点,
∴AE=ED.
在△AEB和△DEC中,
$\left\{\begin{array}{l}{AE=ED}\\{∠A=∠D}\\{AB=DC}\end{array}\right.$,
∴△AEB≌△DEC.
∴BE=EC.
∵H、F分别是BC和EC的中点,
∴HF=$\frac{1}{2}EB$.
同理:$GF=\frac{1}{2}EC$.
∵G,H分别是EB,EC的中点,
∴EG=$\frac{1}{2}$BE,EH=$\frac{1}{2}EC$.
∵BE=EC,
∴EG=GF=FH=EH.
∴四边形EGFH菱形.
点评 本题主要考查的是菱形的判定、等腰梯形的性质、三角形的中位线定理、全等三角形的判定,证得BE=EC是解题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 如图,在?ABCD中,点E,F分别在边AD,BC上,且BF=DE,AF与DC的延长线交于点H,CE与BA的延长线交于点G,求证:AC与GH互相平分.
如图,在?ABCD中,点E,F分别在边AD,BC上,且BF=DE,AF与DC的延长线交于点H,CE与BA的延长线交于点G,求证:AC与GH互相平分. 如图,△ABC中,BO,CO分别平分∠ABC和∠ACB
如图,△ABC中,BO,CO分别平分∠ABC和∠ACB 如图,四边形AOBC是平行四边形,A(-2,0),B(4,2$\sqrt{3}$),反比例函数y=$\frac{n}{x}$的图象经过点C.
如图,四边形AOBC是平行四边形,A(-2,0),B(4,2$\sqrt{3}$),反比例函数y=$\frac{n}{x}$的图象经过点C.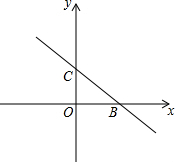 如图,已知直线y=-$\frac{2}{3}$x+2与x轴、y轴分别相交于点B、点C
如图,已知直线y=-$\frac{2}{3}$x+2与x轴、y轴分别相交于点B、点C
