题目内容
1.如图,已知⊙A过原点O且与x轴交于点C(6,0),与y轴交于点B(0,8),直线y=kx(k>0)与⊙A交于另一点P,连接线段PC.(1)线段OP长度的最大值为10,tan∠OPC=$\frac{3}{4}$;
(2)当k=1时,求点P的坐标;
(3)设过点O,C的抛物线y=ax(x-6)的顶点为Q,问是否同时存在a,k的值,使得以O,C,Q为顶点的三角形与△OCP相似?若存在,求出a,k的值;若不存在,请说明理由.
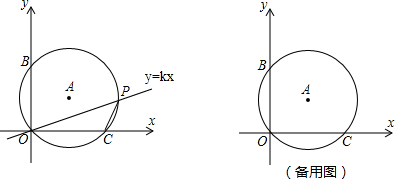
分析 (1)首先作AD⊥y轴于点D,作AE⊥x轴于点E,求出⊙A的半径是多少;然后根据当线段OP为圆的直径时,求出线段OP长度的最大值为多少,进而求出tan∠OPC的值是多少即可.
(2)首先作PN⊥x轴于N,CM⊥OP于M,在Rt△OMC中,求出OM的值是多少;然后在Rt△PMC中,tan∠OPC=$\frac{OM}{MP}=\frac{3}{4}$,求出MP、OP的值各是多少,进而求出点P的坐标是多少即可.
(3)根据题意,分三种情况:①当△OPC∽△QOC时;②当△COP∽△QOC时;③当△POC∽△QOC时;然后分类讨论,根据以O,C,Q为顶点的三角形与△OCP相似,求出a,k的值是多少即可.
解答 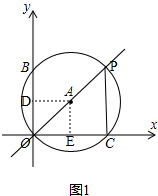 解:(1)如图1,作AD⊥y轴于点D,作AE⊥x轴于点E,
解:(1)如图1,作AD⊥y轴于点D,作AE⊥x轴于点E,
∵AD=$\frac{1}{2}OC=\frac{1}{2}×6=3$,AE=$\frac{1}{2}OB=\frac{1}{2}×8=4$,
∴⊙A的半径r=$\sqrt{{3}^{2}{+4}^{2}}=5$,
∴当线段OP为圆的直径时,
线段OP长度的最大值为:2r=2×5=10,
此时tan∠OPC=$\frac{OC}{PC}=\frac{6}{\sqrt{{10}^{2}{-6}^{2}}}=\frac{6}{8}=\frac{3}{4}$.
(2)如图2,作PN⊥x轴于N,CM⊥OP于M,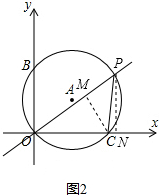
当k=1时,
在Rt△OMC中,∠MOC=45゜,OC=6,
∴OM=MC=$3\sqrt{2}$,
在Rt△PMC中,tan∠OPC=$\frac{OM}{MP}=\frac{3}{4}$,
∴MP=$4\sqrt{2}$,
∴OP=$3\sqrt{2}$+$4\sqrt{2}$=$7\sqrt{2}$,
在Rt△PMC中,PN=ON=7,
∴点P的坐标是(7,7).
(3)∵抛物线y=ax(x-6)=a(x-3﹚2-9a,
∴Q点的坐标为:(3,-9a),且QO=QA;
假设同时存在a,k的值,使得以O,C,Q为顶点的三角形与△OCP相似,
①当△OPC∽△QOC时,
此时k<0,不符合题意;
②如图3,当△COP∽△QOC时,作PM⊥x轴于点M,作QN⊥x轴于点N,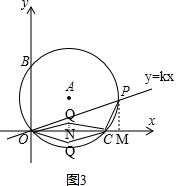
∵$\frac{CO}{QO}=\frac{CP}{QC}$,
∴$\frac{CO}{CP}=\frac{QO}{QC}=1$,
∴∠POC=∠P,∠QOC=∠POC=∠P;
则ON=$\frac{1}{2}OC=\frac{1}{2}×6=3$,
则$\frac{QN}{ON}=tan∠QOC=tan∠OPC$=$\frac{3}{4}$,
∴QN=ON×$\frac{3}{4}=\frac{9}{4}$,
∴|-9a|=$\frac{9}{4}$,
解得a=$\frac{1}{4}$或a=-$\frac{1}{4}$,
此时k=$\frac{PM}{OM}$=tan∠POC=tan∠OPC=$\frac{3}{4}$.
③如图4,当△POC∽△QOC时,作PM⊥x轴于M,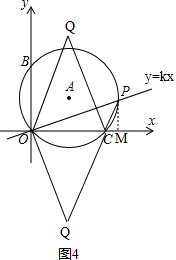
Q与P重合或关于x轴对称,
∵以B(0,8),C(6,0)为为端点的线段是圆A的直径,
∴A点的坐标是(3,4),
∴OM=3,PM=AM+AP=4+5=9,k=$\frac{PM}{0M}$=3,
此时,|-9a|=9,
解得a=1或a=-1.
综上,可得
同时存在a,k的值,使得以O,C,Q为顶点的三角形与△OCP相似,
当k=$\frac{3}{4}$时,a=$\frac{1}{12}$或a=-$\frac{1}{12}$;当k=3时,a=1或a=-1.
故答案为:10;$\frac{3}{4}$.
点评 (1)此题主要考查了圆的综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用.
(2)此题还考查了相似三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | 15 | B. | 30 | C. | 60 | D. | 120 |
| A. | 2,3,4 | B. | 1,4,9 | C. | 1,$\frac{1}{2}$,$\frac{1}{3}$ | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
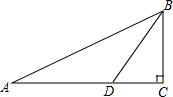 如图,在△ABC中,∠C=90°,点D在边AC上,且∠DBC=∠A,若AC=25,tanA=$\frac{2}{5}$.
如图,在△ABC中,∠C=90°,点D在边AC上,且∠DBC=∠A,若AC=25,tanA=$\frac{2}{5}$.
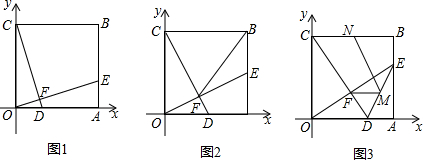 如图1,在平面直角坐标系中,OABC是边长为1的正方形,E是AB上一动点,D是OA上一动点,且OD=AE,OE与CD交于点F.
如图1,在平面直角坐标系中,OABC是边长为1的正方形,E是AB上一动点,D是OA上一动点,且OD=AE,OE与CD交于点F.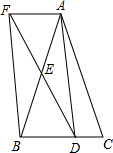 如图,在△ABC中,点D、E分别是BC、AB边的中点,过A点作AF∥BC交DE的延长线于F点,连接AD、BF.
如图,在△ABC中,点D、E分别是BC、AB边的中点,过A点作AF∥BC交DE的延长线于F点,连接AD、BF.