题目内容
20.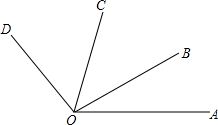 如图,已知∠AOB是∠AOC的余角,∠AOD是∠AOC的补角,且∠BOC=$\frac{1}{2}$∠BOD,求∠AOC和∠BOD的度数.
如图,已知∠AOB是∠AOC的余角,∠AOD是∠AOC的补角,且∠BOC=$\frac{1}{2}$∠BOD,求∠AOC和∠BOD的度数.
分析 根据余角和补角的定义可得∠AOB+∠AOC=90°,∠AOD+∠AOC=180°,∠BOD=∠AOD-∠AOB,等量代换可得∠BOD,∠AOC.
解答 解:∵∠AOB+∠AOC=90°,∠AOD+∠AOC=180°,
∴∠AOB=90°-∠AOC,∠AOD=180°-∠AOC,
∵∠BOD=∠AOD-∠AOB=(180°-∠AOC)-(90°-∠AOC)=90°,
∵∠BOC=$\frac{1}{2}$∠BOD,
∴∠BOC=$\frac{1}{2}$×90°=45°,
∵∠AOC=∠AOB+∠BOC=(90°-∠AOC)+45°,
∴∠AOC=67.5°.
点评 本题主要考查了余角和补角的定义,利用定义和等量代换是解答此题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
11.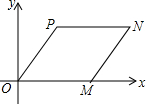 如图所示,在平行直角坐标系中,?OMNP的顶点P坐标是(3,4),顶点M坐标是(4,0)、则顶点N的坐标是( )
如图所示,在平行直角坐标系中,?OMNP的顶点P坐标是(3,4),顶点M坐标是(4,0)、则顶点N的坐标是( )
 如图所示,在平行直角坐标系中,?OMNP的顶点P坐标是(3,4),顶点M坐标是(4,0)、则顶点N的坐标是( )
如图所示,在平行直角坐标系中,?OMNP的顶点P坐标是(3,4),顶点M坐标是(4,0)、则顶点N的坐标是( )| A. | N(7,4) | B. | N(8,4) | C. | N(7,3) | D. | N(8,3) |
4.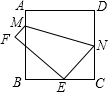 如图所示,将边长为6cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )
如图所示,将边长为6cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )
 如图所示,将边长为6cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )
如图所示,将边长为6cm的正方形纸片ABCD折叠,使点D落在BC中点E处,点A落在F处,折痕为MN,则线段CN的长是( )| A. | 2.25 | B. | 3 | C. | 4 | D. | 4.5 |
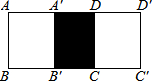 如图,长方形ABCD中,AB=6cm,BC=9cm,把长方形ABCD水平向右平移得到长方形A′B′C′D′,若重叠部分的面积为24cm2,则平移的距离是6cm.
如图,长方形ABCD中,AB=6cm,BC=9cm,把长方形ABCD水平向右平移得到长方形A′B′C′D′,若重叠部分的面积为24cm2,则平移的距离是6cm.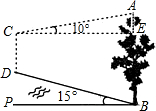 如图,山脚下有一棵树AB,小华从点B沿坡角为15°的坡面上行走50m到达点D,用高为1.5m的测角仪CD测得树顶A的仰角为10°,求树高AB(精确到0.1m)
如图,山脚下有一棵树AB,小华从点B沿坡角为15°的坡面上行走50m到达点D,用高为1.5m的测角仪CD测得树顶A的仰角为10°,求树高AB(精确到0.1m)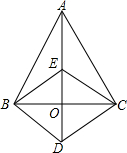 如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE
如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE