题目内容
5.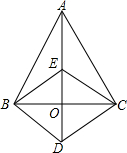 如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE
如图,△ABC中,O是边BC的中点,点D是AD延长线上一点,BE∥CD交AD于E,连接BD、CE(1)求证:四边形BECD是平行四边形;
(2)若AB=AC=2$\sqrt{5}$,BC=4,当点D在AD延长线上移动时,四边形BECD能否成为正方形?若能,求出AD的长;若不能,说明理由.
分析 (1)由BE∥CD得到∠EBO=∠DCO,再利用“ASA”证明△OBE≌△OCD得到BE=CD,于是可判断四边形BECD是平行四边形;
(2)由于AB=AC=2$\sqrt{5}$,OB=OC=2,根据等腰三角形的性质得AO⊥BC,于是可判定四边形BECD为菱形,根据正方形的判定方法,当OD=OB=2时,四边形BECD为正方形,接着利用勾股定理计算出OA=4,所以AD=AO+OD=6.
解答 (1)证明:∵BE∥CD,
∴∠EBO=∠DCO,
∵O是边BC的中点,
∴OB=OC,
在△OBE和△OCD中,
$\left\{\begin{array}{l}{∠EBO=∠DCO}\\{OB=OC}\\{∠BOE=∠COD}\end{array}\right.$,
∴△OBE≌△OCD,
∴BE=CD,
而BE∥CD,
∴四边形BECD是平行四边形;
(2)解:存在.
∵AB=AC=2$\sqrt{5}$,OB=OC=2,
∴AO⊥BC,
∴四边形BECD为菱形,
当OD=OB=2时,四边形BECD为正方形,
在Rt△ABO中,OA=$\sqrt{(2\sqrt{5})^{2}-{2}^{2}}$=4,
∴AD=AO+OD=4+2=6.
点评 本题考查了正方形的判定:先判定四边形是矩形,再判定这个矩形有一组邻边相等;先判定四边形是菱形,再判定这个矩形有一个角为直角.也考查了平行四边形的判定.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
8.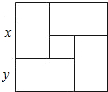 用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )
用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )
 用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )
用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽,已知大正方形的面积是121,小正方形的面积是9,若用x,y(x>y)表示长方形的长和宽,则下列关系中不正确的是( )| A. | x+y=11 | B. | x2+y2=180 | C. | x-y=3 | D. | x•y=28 |
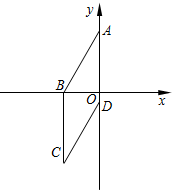 如图,四边形ABCD为菱形,已知A(0,4),B(-3,0),点D在y轴上.求点D的坐标和对角线AC的长.
如图,四边形ABCD为菱形,已知A(0,4),B(-3,0),点D在y轴上.求点D的坐标和对角线AC的长.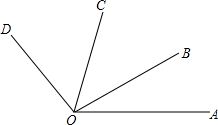 如图,已知∠AOB是∠AOC的余角,∠AOD是∠AOC的补角,且∠BOC=$\frac{1}{2}$∠BOD,求∠AOC和∠BOD的度数.
如图,已知∠AOB是∠AOC的余角,∠AOD是∠AOC的补角,且∠BOC=$\frac{1}{2}$∠BOD,求∠AOC和∠BOD的度数. 如图,将面积为a2的正方形ADGF与面积为b2的正方形BGCE放在一起(b>a>0),试用a、b表示三角形ABC的面积.
如图,将面积为a2的正方形ADGF与面积为b2的正方形BGCE放在一起(b>a>0),试用a、b表示三角形ABC的面积.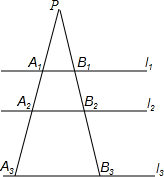 如图,l1∥l2∥l3,B1B2=$\frac{1}{2}$B2B3,又A1B1=1,A3B3=3,则A2B2=$\frac{5}{3}$,$\frac{P{A}_{1}}{{A}_{1}{A}_{2}}$=$\frac{3}{2}$.
如图,l1∥l2∥l3,B1B2=$\frac{1}{2}$B2B3,又A1B1=1,A3B3=3,则A2B2=$\frac{5}{3}$,$\frac{P{A}_{1}}{{A}_{1}{A}_{2}}$=$\frac{3}{2}$.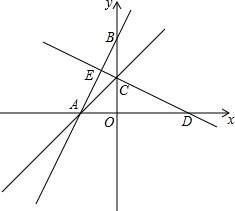 如图,在平面直角坐标系中,直线y=2x+4交x轴于点A,交Y轴于点B,点C为BO中点.
如图,在平面直角坐标系中,直线y=2x+4交x轴于点A,交Y轴于点B,点C为BO中点.