题目内容
8．
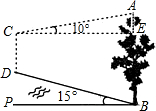如图，山脚下有一棵树AB，小华从点B沿坡角为15°的坡面上行走50m到达点D，用高为1.5m的测角仪CD测得树顶A的仰角为10°，求树高AB（精确到0.1m）（已知sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin15°≈0.26，cos15°≈0.97，tan15°≈0.27）
分析 由已知可得BD=50m，CD∥AB．要求AB的长可以延长CD交水平面与点F．则AB=AE+BE=AE+CD+DF，问题转化为求DF、AE，转化为解直角三角形．
解答 
解：延长CD交PB于F，则DF⊥PB．
∴在直角△DFB中，DF=BD•sin15°≈50×0.26=13.0m
CE=BF=BD•cos15°≈50×0.97=48.5m
∴AE=CE•tan10°≈48.5×0.18=8.73m．
∴AB=AE+CD+DF=8.73+1.5+13=23.2m．
答：树高约为23.2m．
点评 本题考查的是解直角三角形的应用，通过作高线把梯形转化为解直角三角形和矩形的问题是解题的关键．
练习册系列答案
相关题目
19．下列每组数表示三根小木棒的长度，三根小棒能摆成三角形的一组是（ ）
| A． | 1cm，2cm，3cm | B． | 2cm，3cm，4cm | C． | 2cm，3cm，5cm | D． | 2cm，3cm，6cm |
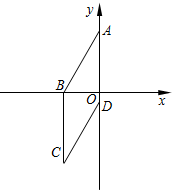如图，四边形ABCD为菱形，已知A（0，4），B（-3，0），点D在y轴上．求点D的坐标和对角线AC的长．
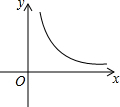如图所示，是反比例函数y=$\frac{m-3}{x}$的图象上的一支，根据图象回答下列问题：
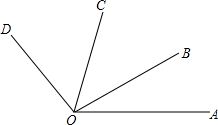如图，已知∠AOB是∠AOC的余角，∠AOD是∠AOC的补角，且∠BOC=$\frac{1}{2}$∠BOD，求∠AOC和∠BOD的度数．
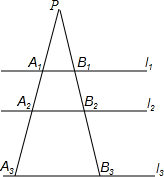如图，l1∥l2∥l3，B1B2=$\frac{1}{2}$B2B3，又A1B1=1，A3B3=3，则A2B2=$\frac{5}{3}$，$\frac{P{A}_{1}}{{A}_{1}{A}_{2}}$=$\frac{3}{2}$．
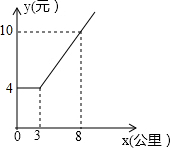某市出租车公司收费标准如图所示，