题目内容
13.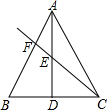 如图所示,AD是△ABC的中线.
如图所示,AD是△ABC的中线.(1)若E为AD的中点,射线CE交AB于F,求$\frac{AF}{BF}$;
(2)若E为AD上的一点,且$\frac{AE}{ED}$=$\frac{1}{k}$,射线CE交AB于F,求$\frac{AF}{BF}$.
分析 (1)作DG∥CF交AB于G,由平行线分线段成比例定理得出FG=BG,BF=2FG,AF=FG,得出AF=FG=BG,即可得出结果;
(2)作DG∥CF交AB于G,由平行线分线段成比例定理得出FG=BG,BF=2FG,$\frac{AF}{FG}=\frac{AE}{ED}$=$\frac{1}{k}$,即可得出结果.
解答 解:(1)作DG∥CF交AB于G,如图1所示:
∵AD是△ABC的中线,
∴BD=CD,
∵DG∥CF,
∴FG=BG,BF=2FG,
∵E为AD的中点,
∴AF=FG,
∴AF=FG=BG,
∴$\frac{AF}{BF}$=$\frac{1}{2}$;
(2)作DG∥CF交AB于G,如图2所示:
∵AD是△ABC的中线,
∴BD=CD,
∵DG∥CF,
∴FG=BG,BF=2FG,$\frac{AF}{FG}=\frac{AE}{ED}$=$\frac{1}{k}$,
∴$\frac{AF}{BF}=\frac{AF}{2FG}$=$\frac{1}{2k}$.
点评 本题考查了平行线分线段成比例定理;熟练掌握平行线分线段成比例定理,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
18. 如图,CD为⊙O的直径,CD⊥EF,垂点为G,∠EOD=40°,则∠DCF=( )
如图,CD为⊙O的直径,CD⊥EF,垂点为G,∠EOD=40°,则∠DCF=( )
 如图,CD为⊙O的直径,CD⊥EF,垂点为G,∠EOD=40°,则∠DCF=( )
如图,CD为⊙O的直径,CD⊥EF,垂点为G,∠EOD=40°,则∠DCF=( )| A. | 80° | B. | 50° | C. | 40° | D. | 20° |
5.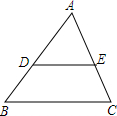 如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( )
如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( )
 如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( )
如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( )| A. | 3:2 | B. | 3:5 | C. | 9:25 | D. | 9:16 |
2.不等式-3(x+2)>a+2的解是负数,则a的取值范围是( )
| A. | a≥-3 | B. | a≥-10 | C. | a≥-8 | D. | a<0 |
3.下列各式中正确的是( )
| A. | -3.14<-π | B. | 1.5>-1 | C. | -3.5>-3.4 | D. | -0.5<-2 |
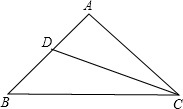 如图,△ABC中,∠A=90°,CD平分∠ACB,若AD=1,AC=2,BC=$\frac{10}{3}$,求△ABC的面积.
如图,△ABC中,∠A=90°,CD平分∠ACB,若AD=1,AC=2,BC=$\frac{10}{3}$,求△ABC的面积.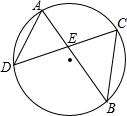 如图,AD=BC,求证:AB=DC,BE=DE.
如图,AD=BC,求证:AB=DC,BE=DE.