如图.若点M是线段AC的中点.N是线段BC的中点.且AB=8.CN=1.5.则AM=( )A．2B．3C．2.5D．1.5 题目和参考答案——青夏教育精英家教网—

题目内容

2．

如图，若点M是线段AC的中点，N是线段BC的中点，且AB=8，CN=1.5，则AM=（　　）

A．

B．

C．

2.5

D．

1.5

分析根据CN的长先求出BC的长，然后得到AC的长，进而求出AM的长．

解答解：∵N是线段BC的中点，CN=1.5，
∴BC=2CN=3，
又∵AB=8，
∴AC=AB-BC=8-3=5，
又∵点M是线段AC的中点，
∴AM=$\frac{1}{2}$AC=2.5，
故选C．

点评此题主要考查了线段的中点的性质，解答此题的关键是找到线段之间的关系．

练习册系列答案

相关题目

12．

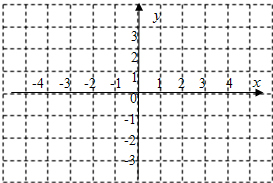如图，方格纸中每个小方格都是边长为1个单位长度的正方形，已知点A（-1，1），现将A点先向左平移3个单位，再向下平移4个单位得到点B，然后作点B关于y轴的对称点得到C点，最后做点C关于x轴的对称点得到D点．
（1）在坐标系中作出点A、B、C、D；
（2）顺次连接ABCDA，求四边形ABCD的面积．

13．（1）解不等式组：$\left\{\begin{array}{l}{2x-1＞-5}\\{-x+1≥2}\end{array}\right.$，并把解集表示在数轴上．
（2）解方程：x²-2x-1=0．

10．

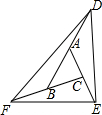如图，在△ABC中，延长BA使BA=AD，延长AC，使AC=CE，延长CB使CB=BF，则下列结论：①若S_△ABC=1，则S_△DFB=2； ②S_△DFB=S_△CEF=S_△AED；③△ABC∽△DEF，其中，正确的个数为（　　）

17．

推理填空：
（1）∵AD∥BC，
∴∠FAD=_∠ABC；
（2）∵∠1=∠2，
∴AB∥CD；
（3）∵AD∥BC，
∴∠3=∠4．

7．解不等式组：$\left\{\begin{array}{l}3x+2＜5（x+1）\\ \frac{1}{3}x-1≤5-\frac{5}{3}x\end{array}\right.$，并将解集在数轴上表示出来．

14．

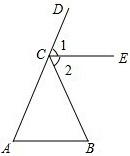如图，给出下面3个论断：AB∥CE，∠1=∠2，∠A=∠B，请从中选取2个论断作为已知，另一个作为结论，组成一个真命题，并证明．
我组成的真命题是：如果∠1=∠2，∠A=∠B，那么AB∥CE．
证明：∵∠DCB=∠A+∠B，且∠DCB=∠1+∠2，
∴∠A+∠B=∠1+∠2，
又∠A=∠B，∠1=∠2，
∴2∠A=2∠1，
∴∠1=∠A，
∴AB∥CE．．

11．（1）已知a^3m=3，b³ⁿ=2，求（a^2m）³+（bⁿ）³-a^2m•bⁿ•a^4m•b²ⁿ的值．
（2）已知z²=x²+y²，化简（x+y+z）（x+y-z）（x-y+z）（-x+y+z）．

12．已知菱形ABCD，点E、F分别在BC、CD上，且△AEF恰为等边三角形，其边长与菱形边长相等，则∠AEB的大小是（　　）

试题分类