题目内容
14.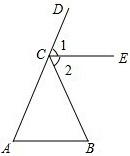 如图,给出下面3个论断:AB∥CE,∠1=∠2,∠A=∠B,请从中选取2个论断作为已知,另一个作为结论,组成一个真命题,并证明.
如图,给出下面3个论断:AB∥CE,∠1=∠2,∠A=∠B,请从中选取2个论断作为已知,另一个作为结论,组成一个真命题,并证明.我组成的真命题是:如果∠1=∠2,∠A=∠B,那么AB∥CE.
证明:∵∠DCB=∠A+∠B,且∠DCB=∠1+∠2,
∴∠A+∠B=∠1+∠2,
又∠A=∠B,∠1=∠2,
∴2∠A=2∠1,
∴∠1=∠A,
∴AB∥CE..
分析 由∠1=∠2,∠A=∠B,利用三角形外角的性质可得出∠1=∠A,可证明AB∥CE,故可选择由∠1=∠2,∠A=∠B证明AB∥CE.
解答 真命题是:如果∠1=∠2,∠A=∠B,那么AB∥CE.
证明:
∵∠DCB=∠A+∠B,且∠DCB=∠1+∠2,
∴∠A+∠B=∠1+∠2,
又∠A=∠B,∠1=∠2,
∴2∠A=2∠1,
∴∠1=∠A,
∴AB∥CE.
故答案为:∠1=∠2,∠A=∠B;AB∥CE;
∵∠DCB=∠A+∠B,且∠DCB=∠1+∠2,
∴∠A+∠B=∠1+∠2,
又∠A=∠B,∠1=∠2,
∴2∠A=2∠1,
∴∠1=∠A,
∴AB∥CE.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
2. 如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
 如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )| A. | 2 | B. | 3 | C. | 2.5 | D. | 1.5 |
9.二次函数y=(x-1)2+3的最小值是( )
| A. | 1 | B. | -1 | C. | -3 | D. | 3 |
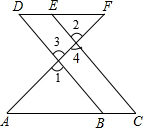 如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.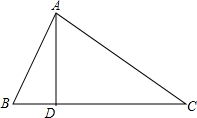 如图,三角形ABC中,AB=10,AC=17,AD与BC交于点D,AD=8,BD=6,求BC的长.
如图,三角形ABC中,AB=10,AC=17,AD与BC交于点D,AD=8,BD=6,求BC的长.