题目内容
12.已知菱形ABCD,点E、F分别在BC、CD上,且△AEF恰为等边三角形,其边长与菱形边长相等,则∠AEB的大小是( )| A. | 60° | B. | 95° | C. | 80° | D. | 75° |
分析 根据菱形的对角相等可得∠B=∠D,再根据等角三角形两底角相等,利用三角形的内角和等于180°表示出∠BAE和∠DAF,然后根据菱形的两邻角互补列式求解即可.
解答 解:如图所示: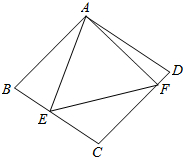 ∵四边形ABCD是菱形,△AEF为等边三角形,
∵四边形ABCD是菱形,△AEF为等边三角形,
∴∠B=∠D,AB=AD,AE=AF,∠EAF=60°,
∵正△AEF的边长与菱形ABCD的边长相等,
∴AB=AE,
∴AB=AE=AD=AF,
∴∠B=∠AEB,∠D=∠AFD,
∴∠BAE=180°-2∠AEB,∠DAF=180°-2∠AFD,
又∵∠EAF=60°,
∴180°-2∠AEB+60°+180°-2∠D+∠D=180°,
整理得,3∠AEB=240°,
解得∠AEB=80°.
故答案为:80°.
点评 本题考查了菱形的性质、等腰三角形两底角相等的性质、等边三角形的性质;根据菱形的邻角互补列出方程是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
2. 如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
 如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )| A. | 2 | B. | 3 | C. | 2.5 | D. | 1.5 |
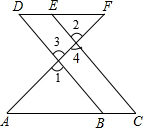 如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D. 如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;
如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;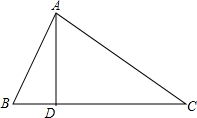 如图,三角形ABC中,AB=10,AC=17,AD与BC交于点D,AD=8,BD=6,求BC的长.
如图,三角形ABC中,AB=10,AC=17,AD与BC交于点D,AD=8,BD=6,求BC的长. △ABC中,∠B=30°,AB=8cm,BC=4cm,则△ABC的面积为8cm2.
△ABC中,∠B=30°,AB=8cm,BC=4cm,则△ABC的面积为8cm2.