题目内容
10.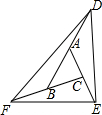 如图,在△ABC中,延长BA使BA=AD,延长AC,使AC=CE,延长CB使CB=BF,则下列结论:①若S△ABC=1,则S△DFB=2; ②S△DFB=S△CEF=S△AED;③△ABC∽△DEF,其中,正确的个数为( )
如图,在△ABC中,延长BA使BA=AD,延长AC,使AC=CE,延长CB使CB=BF,则下列结论:①若S△ABC=1,则S△DFB=2; ②S△DFB=S△CEF=S△AED;③△ABC∽△DEF,其中,正确的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①根据等底等高的三角形的面积相等,可得△ABC与△ABF的关系,△ABF与△ADF的关系,再根据三角形面积的和差,可得答案;
②根据等底等高的三角形的面积相等,可得△ABC与△ABF的关系,△ABC与△ADE的关系,△ABC与△CEF的关系,可得答案;
③根据全等三角形的判定与性质,可得∠CFE与∠AED的关系,根据三角形外角的性质,可得∠ACB与∠DEF的关系,根据相似三角形的判定,可得答案.
解答 解:①连接AF,由FB=BC,等底等高的三角形的面积相等,得
S△ABC=S△ABF=1.
由AB=AD,等底等高的三角形的面积相等,得
S△ABF=S△ADF,
由三角形面积的和差,得
SDFB=SABF+S△ADF=2S△ABC=2,故①正确;
②同理S△AED=2S△ABC,S△CEF=2SABC,
∴S△AED=S△CEF=S△DFB,故②正确;
③∵△ABC不是等边三角形,
∴△CFE与△AED不全等,
∴∠CFE≠∠AED,
∵∠ACB是△CEF的外角,
∴∠ACB=∠CFE+∠CEF≠∠CEF+∠AED,
即∠ACB≠∠DEF,
同理∠ABC≠∠DFE,
∴△ABC与△DFE不相似,故③错误.
故选:C.
点评 本题考查了相似三角形的判定,利用了等底等高三角形面积的关系,全等三角形的判定与性质,相似三角形的判定与性质.

练习册系列答案
相关题目
15.一个水池有甲、乙两个进水管,单独开甲、乙管各需要x小时、y小时可注满水池,现两管同时打开,则注满空池的时间为( )
| A. | $\frac{x+y}{xy}$小时 | B. | $\frac{xy}{x+y}$小时 | C. | $\frac{1}{x+y}$小时 | D. | $\frac{1}{xy}$小时 |
2. 如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
 如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )
如图,若点M是线段AC的中点,N是线段BC的中点,且AB=8,CN=1.5,则AM=( )| A. | 2 | B. | 3 | C. | 2.5 | D. | 1.5 |
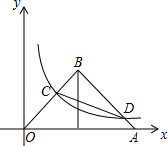 如图,△OAB是等要直角三角形,∠B=90°,BO=BA,OA=4,点O是坐标原点,点A在x轴的正半轴上,双曲线y=$\frac{k}{x}$过OB的中点C且与AB交于点D,连接CD,则∠BDC=30°.
如图,△OAB是等要直角三角形,∠B=90°,BO=BA,OA=4,点O是坐标原点,点A在x轴的正半轴上,双曲线y=$\frac{k}{x}$过OB的中点C且与AB交于点D,连接CD,则∠BDC=30°. 用8块相同的长方形地砖拼成一块巨型地面,地砖的拼放方式及相关数据如图所示,利用所学知识求每块地砖的长和宽.
用8块相同的长方形地砖拼成一块巨型地面,地砖的拼放方式及相关数据如图所示,利用所学知识求每块地砖的长和宽. 如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;
如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;