题目内容
今年中考结束后,我与同学们交流了宁波中考数学卷的压轴题,最后我们一致认为,这道题用了一个简单而重要的数学模型“三垂直型”,其实这种“模型”大家并不陌生.
如图1,AO⊥BO且AO=BO,由点A和点B向过O点的直线作垂线,可以构成如图两个全等三角形;当这条直线绕点O旋转到直角内部时,仍然能构造出全等三角形!相信同学们认识了这个“模型”的特点后,一定能解决下面的问题:
(1)如图3,AD⊥CD,AD⊥AB,若AB=4,CD=6,BC=BE(可以借助图中的辅助线,也可以根据自己所悟,另外画辅助线),你得到阴影部分的面积是: .
(2)如图4,点D是Rt△ABC的平分线任一点,连结DA,作DE⊥DA交另一边BC于点E,若DB长是4
,AD=DE,则四边形ABED的面积值是: .
(3)如图5,点B是两个等腰直角三角形的公共顶点,连结DC和AF,若BE⊥CD交CD于E点,延长EB交AF于G点,试证明AG=GF.
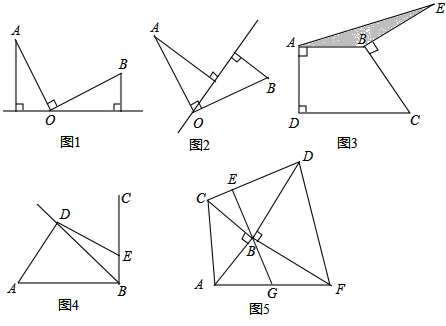
如图1,AO⊥BO且AO=BO,由点A和点B向过O点的直线作垂线,可以构成如图两个全等三角形;当这条直线绕点O旋转到直角内部时,仍然能构造出全等三角形!相信同学们认识了这个“模型”的特点后,一定能解决下面的问题:
(1)如图3,AD⊥CD,AD⊥AB,若AB=4,CD=6,BC=BE(可以借助图中的辅助线,也可以根据自己所悟,另外画辅助线),你得到阴影部分的面积是:
(2)如图4,点D是Rt△ABC的平分线任一点,连结DA,作DE⊥DA交另一边BC于点E,若DB长是4
| 2 |
(3)如图5,点B是两个等腰直角三角形的公共顶点,连结DC和AF,若BE⊥CD交CD于E点,延长EB交AF于G点,试证明AG=GF.

考点:全等三角形的判定与性质
专题:
分析:(1)求出△BFC≌△BHE,推出CF=EH,求出CF即可;
(2)证△AHD≌△EFD,推出DF=DH,得出正方形DFBH,求出DH长,求出四边形ABED面积=正方形DHBF面积即可;
(3)求出AF′=BE=FH,根据全等即可得出答案.
(2)证△AHD≌△EFD,推出DF=DH,得出正方形DFBH,求出DH长,求出四边形ABED面积=正方形DHBF面积即可;
(3)求出AF′=BE=FH,根据全等即可得出答案.
解答: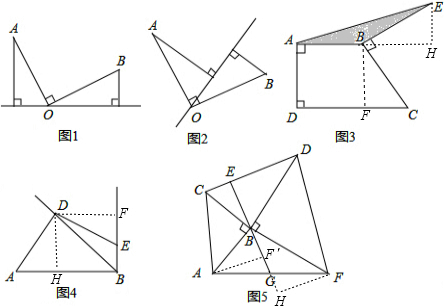
解:(1)过B作BF⊥DC于F,过E作EH⊥AB于H,
则AB=DF=4,∠BFC=∠H=∠FBH=90°
∵DC=6,
∴CF=2,
∵∠EBC=∠FBH=90°,
∴∠EBH=∠CBF,
在△BHE和△BFC中
∴△BHE≌△BFC(AAS),
∴EH=CF=2,
∴阴影部分的面积是
×4×2=4,
故答案为:4;
(2)过D作DH⊥AB于H,DF⊥BE于F,
则DF=BH,∠DHA=∠DHB=∠EBA=∠DFB=90°,
∴四边形DHBF是矩形,
∵BD平分∠ABE,DF⊥BE,DH⊥AB,
∴DH=DF,
∴四边形DHBF是正方形,
∴DH=BH=DF=BF,
∵BD=4
,∠DHB=90°,
∴DH=DF=BH=BF=4,
∵在△ADH和△EDF中
∴△ADH≌△EDF(AAS),
∴S四边形ABED=S△ADH+S四边形DHBE=S△FDE+S四边形DHBE=S正方形DHBF=4×4=16,
故答案为:16;
(3)证明:过A作AF′⊥EG于F′,过F作FH⊥EG于H,
∵∠BEC=∠ABC=∠AF′B=90°,
∴∠ECB+∠CBE=90°,∠CBE+∠ABF′=90°,
∴∠ECB=∠ABF′,
在△BEC和△AF′B中
∴△BEC≌△AF′B(AAS),
∴BE=AF′,
同理FH=BE,
∴AF′=FH,
∵AF′⊥EG,FH⊥EG,
∴∠AF′G=∠H,
在△AF′G和△FHG中
∴△AF′G≌△FHG(AAS),
∴AG=GF.

解:(1)过B作BF⊥DC于F,过E作EH⊥AB于H,
则AB=DF=4,∠BFC=∠H=∠FBH=90°
∵DC=6,
∴CF=2,
∵∠EBC=∠FBH=90°,
∴∠EBH=∠CBF,
在△BHE和△BFC中
|
∴△BHE≌△BFC(AAS),
∴EH=CF=2,
∴阴影部分的面积是
| 1 |
| 2 |
故答案为:4;
(2)过D作DH⊥AB于H,DF⊥BE于F,
则DF=BH,∠DHA=∠DHB=∠EBA=∠DFB=90°,
∴四边形DHBF是矩形,
∵BD平分∠ABE,DF⊥BE,DH⊥AB,
∴DH=DF,
∴四边形DHBF是正方形,
∴DH=BH=DF=BF,
∵BD=4
| 2 |
∴DH=DF=BH=BF=4,
∵在△ADH和△EDF中
|
∴△ADH≌△EDF(AAS),
∴S四边形ABED=S△ADH+S四边形DHBE=S△FDE+S四边形DHBE=S正方形DHBF=4×4=16,
故答案为:16;
(3)证明:过A作AF′⊥EG于F′,过F作FH⊥EG于H,
∵∠BEC=∠ABC=∠AF′B=90°,
∴∠ECB+∠CBE=90°,∠CBE+∠ABF′=90°,
∴∠ECB=∠ABF′,
在△BEC和△AF′B中
|
∴△BEC≌△AF′B(AAS),
∴BE=AF′,
同理FH=BE,
∴AF′=FH,
∵AF′⊥EG,FH⊥EG,
∴∠AF′G=∠H,
在△AF′G和△FHG中
|
∴△AF′G≌△FHG(AAS),
∴AG=GF.
点评:本题考查了三角形内角和定理,全等三角形的性质和判定的应用,主要考查学生的推理能力,难度偏大.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
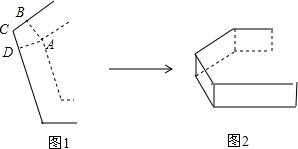 将一个正n边形的纸片(如图1)做成一个高相等且底面为正n边形的无盖纸盒,纸盒的各侧面都与底面垂直(如图2),应在正n边形的每个顶点处剪去一个四边形,如图1中的四边形ABCD是其中的一个,则∠BAD=
将一个正n边形的纸片(如图1)做成一个高相等且底面为正n边形的无盖纸盒,纸盒的各侧面都与底面垂直(如图2),应在正n边形的每个顶点处剪去一个四边形,如图1中的四边形ABCD是其中的一个,则∠BAD=