题目内容
5.阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:$\left\{\begin{array}{l}a=\frac{1}{2}({{m^2}-{n^2}})\\ b=mn\\ c=\frac{1}{2}({{m^2}+{n^2}}).\end{array}\right.$其中m>n>0,m,n是互质的奇数.应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
分析 由n=1,得到a=$\frac{1}{2}$(m2-1)①,b=m②,c=$\frac{1}{2}$(m2+1)③,根据直角三角形有一边长为5,列方程即可得到结论.
解答 解:当n=1,a=$\frac{1}{2}$(m2-1)①,b=m②,c=$\frac{1}{2}$(m2+1)③,
∵直角三角形有一边长为5,
∴Ⅰ、当a=5时,$\frac{1}{2}$(m2-1)=5,解得:m=$±\sqrt{11}$(舍去),
Ⅱ、当b=5时,即m=5,代入①③得,a=12,c=13,
Ⅲ、当c=5时,$\frac{1}{2}$(m2+1)=5,解得:m=±3,
∵m>0,
∴m=3,代入①②得,a=4,b=3,
综上所述,直角三角形的另外两条边长分别为12,13或3,4.
点评 本题考查了勾股定理的逆定理,分类讨论是解题的关键.

练习册系列答案
相关题目
15.已知下列命题:①若|x|=3,则x=3;②当a>b时,若c>0,则ac>bc;③直角三角形中斜边上的中线等于斜边的一半;④内错角相等.
其中原命题与逆命题均为真命题的个数是( )
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是$\frac{1}{7}$.
13.2016年安徽省参加中考的学生数为56.3万人,其中“56.3万”用科学记数法表示为( )
| A. | 5.63×104 | B. | 5.63×105 | C. | 56.3×104 | D. | 0.563×106 |
20.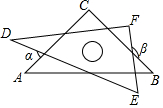 小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
 小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )| A. | 180° | B. | 210° | C. | 360° | D. | 270° |
 如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )
如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )
 某校七年级某班期末测试全班所有学生数学成绩的频数分布直方图如图所示(满分100分),则该班成绩在85.5~95.5这一分数段的学生数是30.
某校七年级某班期末测试全班所有学生数学成绩的频数分布直方图如图所示(满分100分),则该班成绩在85.5~95.5这一分数段的学生数是30.