题目内容
13．不等式组$\left\{\begin{array}{l}{x-1≤3}\\{x+1≤3}\end{array}\right.$的解集在数轴上表示正确的是（ ）| A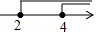． |  | B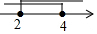． |  | C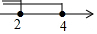． |  | D． |  |
分析 先求出每个不等式的解集，再求出不等式组的解集，最后在数轴上表示出来即可．
解答 解：$\left\{\begin{array}{l}{x-1≤3①}\\{x+1≤3②}\end{array}\right.$
∵解不等式①得：x≤4，
解不等式②得：x≤2，
∴不等式组的解集为x≤2，
在数轴上表示为：
，
故选C．
点评 本题考查了解一元一次不等式组、在数轴上表示不等式组的解集，能根据不等式的解集得出不等式组的解集是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
1．反比例函数$y=\frac{6}{x}$与一次函数y=x+1的图象交于点A（2，3），利用图象的对称性可知它们的另一个交点是（ ）
| A． | （3，2） | B． | （-3，-2） | C． | （-2．-3） | D． | （-2，3） |
8．下列等式成立的是（ ）
| A． | $\frac{1}{2}$=$\frac{b}{2b}$ | B． | $\frac{b}{2b}$=$\frac{1}{2}$ | C． | $\frac{m}{2a}$-$\frac{n}{a}$=$\frac{m-n}{a}$ | D． | a÷b•$\frac{1}{b}$=a |
如图，在平行四边形ABCD中，AB=7，BC=10，∠C的平分线交AD于E，交BA的延长线于F，则AE+AF的值等于（ ）
5．
如图，直线l与x轴、y轴交于点A、B，点C为线段AB上的一动点，过点C分别作CE⊥x轴于点E，作CF⊥y轴于点F．若四边形OECF的周长为6，则直线l的表达式为（ ）
如图，直线l与x轴、y轴交于点A、B，点C为线段AB上的一动点，过点C分别作CE⊥x轴于点E，作CF⊥y轴于点F．若四边形OECF的周长为6，则直线l的表达式为（ ）| A． | y=-x+6 | B． | y=x+6 | C． | y=-x+3 | D． | y=x+3 |
2．
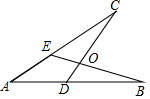如图，点D，E分别在AB，AC上，AD=AE，BE与CD交于点O，下列条件不能判定△ABE≌△ACD的是（ ）
如图，点D，E分别在AB，AC上，AD=AE，BE与CD交于点O，下列条件不能判定△ABE≌△ACD的是（ ）| A． | ∠B=∠C | B． | BE=CD | C． | AB=AC | D． | ∠CEB=∠BDC |
3．下列计算正确的是（ ）
| A． | $\sqrt{3}+\sqrt{3}=2\sqrt{3}$ | B． | $\sqrt{3}+\sqrt{3}=\sqrt{6}$ | C． | $\sqrt{3}×\sqrt{3}=2\sqrt{3}$ | D． | $2+\sqrt{3}=2\sqrt{3}$ |