题目内容
5．
如图，直线l与x轴、y轴交于点A、B，点C为线段AB上的一动点，过点C分别作CE⊥x轴于点E，作CF⊥y轴于点F．若四边形OECF的周长为6，则直线l的表达式为（ ）| A． | y=-x+6 | B． | y=x+6 | C． | y=-x+3 | D． | y=x+3 |
分析 设点C的坐标为（x，y），根据矩形的性质得到CF+CE=3，得到直线l的表达式．
解答 解：设点C的坐标为（x，y），
∵四边形OECF的周长为6，
∴CF+CE=3，
∴|x|+|y|=3，即y=x+3，
∴直线l的表达式为y=x+3，
故选：D．
点评 本题考查的是一次函数解析式的求法，灵活运用待定系数法求一次函数解析式是解题的关键．
练习册系列答案
相关题目
16．下列关系式中，y不是x的函数的是（ ）
| A． | y=x2 | B． | |y|=x | C． | y=2x+1 | D． | y=$\frac{8}{x}$ |
20．
如图，一直线与两坐标轴的正半轴分别交于A、B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20，则该直线的函数表达式是（ ）
如图，一直线与两坐标轴的正半轴分别交于A、B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20，则该直线的函数表达式是（ ）| A． | y=x+10 | B． | y=-x+10 | C． | y=x+20 | D． | y=-x+20 |
10．
如图直线a∥b，若∠1=70°，则∠2为（ ）
如图直线a∥b，若∠1=70°，则∠2为（ ）| A． | 70° | B． | 110° | C． | 70°或110° | D． | 120° |
17．
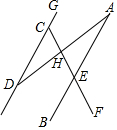如图，下列条件不能判定AB∥CD的是（ ）
如图，下列条件不能判定AB∥CD的是（ ）| A． | ∠BAD=∠ADG | B． | ∠GCE=∠AEF | C． | ∠GDH+∠DHF=180° | D． | ∠FEB+∠GCE=180° |
15．下列运算正确的是（ ）
| A． | a•a2=a2 | B． | （ab）2=ab | C． | 3-1=$\frac{1}{3}$ | D． | $\sqrt{5}+\sqrt{5}=\sqrt{10}$ |