题目内容
2.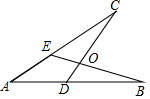 如图,点D,E分别在AB,AC上,AD=AE,BE与CD交于点O,下列条件不能判定△ABE≌△ACD的是( )
如图,点D,E分别在AB,AC上,AD=AE,BE与CD交于点O,下列条件不能判定△ABE≌△ACD的是( )| A. | ∠B=∠C | B. | BE=CD | C. | AB=AC | D. | ∠CEB=∠BDC |
分析 已有条件AD=AE,公共角∠A=∠A,然后根据所给选项,结合全等三角形的判定方法进行分析即可.
解答 解:A、添加∠B=∠C可利用AAS判定△ABE≌△ACD,故此选项错误;
B、添加BE=CD不能判定△ABE≌△ACD,故此选项正确;
C、添加AB=AC可利用SAS判定△ABE≌△ACD,故此选项错误;
D、添加∠CEB=∠BDC可得∠AEB=∠ADC,可利用ASA判定△ABE≌△ACD,故此选项错误;
故选:B.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
12. 如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠BAD′=70°,则α的大小为( )
如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠BAD′=70°,则α的大小为( )
 如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠BAD′=70°,则α的大小为( )
如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠BAD′=70°,则α的大小为( )| A. | 30° | B. | 20° | C. | 15° | D. | 10° |
10. 如图直线a∥b,若∠1=70°,则∠2为( )
如图直线a∥b,若∠1=70°,则∠2为( )
 如图直线a∥b,若∠1=70°,则∠2为( )
如图直线a∥b,若∠1=70°,则∠2为( )| A. | 70° | B. | 110° | C. | 70°或110° | D. | 120° |
17.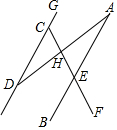 如图,下列条件不能判定AB∥CD的是( )
如图,下列条件不能判定AB∥CD的是( )
 如图,下列条件不能判定AB∥CD的是( )
如图,下列条件不能判定AB∥CD的是( )| A. | ∠BAD=∠ADG | B. | ∠GCE=∠AEF | C. | ∠GDH+∠DHF=180° | D. | ∠FEB+∠GCE=180° |
7. 如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )
如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )
 如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )
如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )| A. | 3m+n=180° | B. | 4m-n=180° | C. | 3m-n=180° | D. | 2m+n=180° |
11.平行四边形所具有的性质是( )
| A. | 对角线相等 | B. | 邻边互相垂直 | ||
| C. | 每条对角线平分一组对角 | D. | 两组对边分别相等 |


 如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于D,tan∠B=$\frac{1}{3}$,且BC=9 cm,求AC,AB及CD的长.
如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于D,tan∠B=$\frac{1}{3}$,且BC=9 cm,求AC,AB及CD的长.