题目内容
16.解方程(1)2-$\frac{2x+1}{3}$=$\frac{1+x}{2}$;
(2)完善下面解方程$\frac{0.3x+0.5}{0.2}$=$\frac{2x-1}{3}$的过程.
解:原方程可变形为$\frac{3x+5}{2}$=$\frac{2x-1}{3}$,(分数的性质 )
去分母,得3(3x+5)=2(2x-1).( 等式性质2 )
去括号,得9x+15=4x-2.(乘法分配律 )
移项,得9x-4x=-15-2.( 等式性质1 )
合并,得5x=-17.( 合并同类项 )系数化为1,得x=-$\frac{17}{5}$.( 等式性质2 )
分析 (1)根据去分母、去括号、移项、合并同类项、系数化为1,可得答案;
(2)根据去分母、去括号、移项、合并同类项、系数化为1,可得答案;
解答 解:(1)去分母,得12-2(2x+1)=3(1+x)
去括号,得12-4x-2=3+3x
移项,得-4x-3x=3-12+2
合并同类项,得-7x=-7
系数互为1,得x=1;
(2)原方程可变形为$\frac{3x+5}{2}$=$\frac{2x-1}{3}$,( 分数的性质 )
去分母,得3(3x+5)=2(2x-1).( 等式性质2 )
去括号,得9x+15=4x-2.( 乘法分配律 )
移项,得9x-4x=-15-2.( 等式性质1 )
合并,得5x=-17.( 合并同类项 )
系数化为1,得x=-$\frac{17}{5}$.( 等式性质2 ),
故答案为:分数的性质,去分母,乘法分配律,移项,系数化为1.
点评 本题考查了解一元一次方程,去分母是解题关键,不含分母的项不要漏乘分母的最小公倍数.

练习册系列答案
相关题目
20.按如图所示的程序计算,若开始输入的n值为 $\sqrt{2}$,则最后输出的结果是( ) 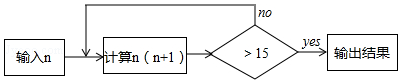

| A. | 14 | B. | 16 | C. | 8+5$\sqrt{2}$ | D. | 14+$\sqrt{2}$ |
11. 如图,A,B,C三点在⊙O上,∠ABC=25°,则∠AOC等于( )
如图,A,B,C三点在⊙O上,∠ABC=25°,则∠AOC等于( )
 如图,A,B,C三点在⊙O上,∠ABC=25°,则∠AOC等于( )
如图,A,B,C三点在⊙O上,∠ABC=25°,则∠AOC等于( )| A. | 25° | B. | 50° | C. | 60° | D. | 70° |
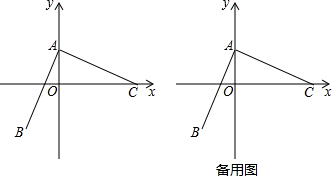
1. 甲、乙两人从同一地点出发到达同一目的地,如图是他们离出发地的路程y(百米)与时间x(分钟)的关系图象,下列结论不正确的是( )
甲、乙两人从同一地点出发到达同一目的地,如图是他们离出发地的路程y(百米)与时间x(分钟)的关系图象,下列结论不正确的是( )
 甲、乙两人从同一地点出发到达同一目的地,如图是他们离出发地的路程y(百米)与时间x(分钟)的关系图象,下列结论不正确的是( )
甲、乙两人从同一地点出发到达同一目的地,如图是他们离出发地的路程y(百米)与时间x(分钟)的关系图象,下列结论不正确的是( )| A. | 甲经过54分钟到达目的地 | |
| B. | 乙比甲晚出发12分钟 | |
| C. | 当乙到达目的地时甲、乙两人所走的路程比为5:9 | |
| D. | 若乙到达目的地后继续往前走,当甲到达目的地时乙比甲多走140米 |
5.4根小木棒的长度分别是2cm,3cm,4cm,5cm,任取其中三根,可以搭出几个不同的三角形( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
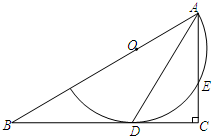 如图,△ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.
如图,△ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.