题目内容
19.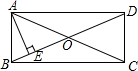 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作BD的垂线,垂足为E,若∠EAD=3∠BAE,则∠AOE=45°.
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点A作BD的垂线,垂足为E,若∠EAD=3∠BAE,则∠AOE=45°.
分析 根据矩形性质求出OA=OB,∠BAD=90°,求出∠BAE=22.5°,∠DAE=67.5°,再求出∠ABO的度数以及∠OAB的度数,得出∠OAE的度数,即可得出结果.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠DAE=3∠BAE,∠BAE+∠DAE=∠BAD,
∴∠BAE=22.5°,∠DAE=67.5°,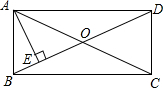
∵AE⊥BD,
∴∠AEB=90°,
∴∠ABO=∠AEB-∠BAE=90°-22.5°=67.5°,
∵四边形ABCD是矩形,
∴AC=BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,
∴OA=OB,
∴∠OAB=∠ABO=67.5°,
∴∠OAE=67.5°-22.5°=45°,
∴∠AOE=90°-∠OAE=45°;
故答案为:45°.
点评 本题考查了矩形性质、等腰三角形性质、三角形的内角和定理;熟练掌握矩形的性质,弄清各个角之间的数量关系是解决问题的关键.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
9. 如图,AD是∠EAC的平分线,AD∥BC,∠C=25°,则∠B为( )
如图,AD是∠EAC的平分线,AD∥BC,∠C=25°,则∠B为( )
 如图,AD是∠EAC的平分线,AD∥BC,∠C=25°,则∠B为( )
如图,AD是∠EAC的平分线,AD∥BC,∠C=25°,则∠B为( )| A. | 45° | B. | 30° | C. | 25° | D. | 20° |
7.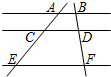 如图,如果AB∥CD∥EF,那么下列结论正确的是( )
如图,如果AB∥CD∥EF,那么下列结论正确的是( )
 如图,如果AB∥CD∥EF,那么下列结论正确的是( )
如图,如果AB∥CD∥EF,那么下列结论正确的是( )| A. | $\frac{AC}{AE}$=$\frac{CD}{EF}$ | B. | $\frac{AC}{BD}$=$\frac{CE}{DF}$ | C. | $\frac{AC}{CE}$=$\frac{AB}{CD}$ | D. | $\frac{AC}{DF}$=$\frac{BD}{CE}$ |
14.已知一元二次方程2x2+x+k=0无实数根,那么反比例函数y=$\frac{k}{x}$的图象位于( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一象限 | D. | 无法确定 |
8.若点(2,9)和(-3,a)都在某反比例函数的图象上,则a的值为( )
| A. | -6 | B. | 6 | C. | -2 | D. | 2 |
 如图,一次函数y=-x+2与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A的横坐标为-2.
如图,一次函数y=-x+2与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A的横坐标为-2. 如图,在等边三角形ABC中AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,若BE=2,则AF=6.
如图,在等边三角形ABC中AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,若BE=2,则AF=6.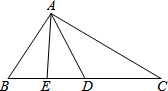 已知,如图,AD是△ABC的中线,AE是△ABD的中线,AB=DC,∠BAD=∠BDA,求证:AC=2AE.
已知,如图,AD是△ABC的中线,AE是△ABD的中线,AB=DC,∠BAD=∠BDA,求证:AC=2AE.