题目内容
7.指出下列抛物线的开口方向、对称轴和顶点坐标,并判断有最大值还是有最小值:(1)y=x2-4x+5;
(2)y=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4;
(3)y=-3x2-2x+1
(4)y=-$\frac{1}{2}$x2+2x+1.
分析 (1)将函数变形为顶点坐标式,再依次判断其各个性质.
(2)将函数变形为顶点坐标式,再依次判断其各个性质.
(3)将函数变形为顶点坐标式,再依次判断其各个性质.
(4)将函数变形为顶点坐标式,再依次判断其各个性质.
解答 解:(1)y=x2-4x+5=(x-2)2+1;
∵a=1>0,
∴开口向上,对称轴x=2,顶点(2,1),y有最小值.
(2)y=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4=-$\frac{1}{4}$(x+3)2+$\frac{25}{4}$
∵a=-$\frac{1}{4}$<0,
∴开口向下,对称轴x=-3,顶点(-3,$\frac{25}{4}$),y有最大值.
(3)y=-3x2-2x+1=-3(x+$\frac{1}{3}$)2+$\frac{4}{3}$
∵a=-3<0,
∴开口向下,对称轴x=-$\frac{1}{3}$,顶点(-$\frac{1}{3}$,$\frac{4}{3}$),y有最大值.
(4)y=-$\frac{1}{2}$x2+2x+1=-$\frac{1}{2}$(x-2)2+3.
∵a=-$\frac{1}{2}$>0,
∴开口向下,对称轴x=2,顶点(2,3),y有最大值.
点评 本题考查了二次函数的性质,是基础题,熟练掌握配方法是以及二次函数的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.柯桥苏宁电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5100元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1720元 |
| 第二周 | 4台 | 10台 | 2960 元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5100元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
16.下列各选项中,∠1和∠2是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,线段AB的端点A、B均在格点上,在正方形网格图①和图②中分别画一个三角形.
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,线段AB的端点A、B均在格点上,在正方形网格图①和图②中分别画一个三角形.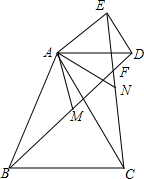 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,A,B,D三点不在同一条直线上.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,A,B,D三点不在同一条直线上.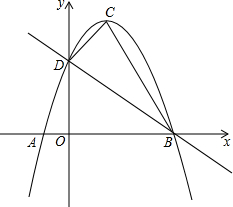 如图,抛物线y=ax2+bx+c的顶点为C(1,4),且与y轴交于点D(0,3),与x轴交于A、B两点.
如图,抛物线y=ax2+bx+c的顶点为C(1,4),且与y轴交于点D(0,3),与x轴交于A、B两点. 小峰家要在一面长为38m的墙的一侧修建4个同样大小的猪圈,并在如图所示的5处各留1.5m宽的门,已知现有的材料共可修建长为41m的墙体,则能修建的4个猪圈的最大面积为$\frac{9409}{80}$.
小峰家要在一面长为38m的墙的一侧修建4个同样大小的猪圈,并在如图所示的5处各留1.5m宽的门,已知现有的材料共可修建长为41m的墙体,则能修建的4个猪圈的最大面积为$\frac{9409}{80}$.