Question

15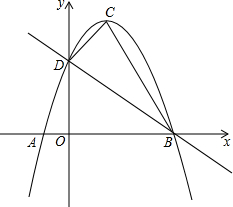．如图，抛物线y=ax²+bx+c的顶点为C（1，4），且与y轴交于点D（0，3），与x轴交于A、B两点．
（1）求此抛物线的解析式；
（2）若直线BD的解析式为y=mx+n，请直接写出不等式ax²+bx+c＞mx+n的解集；
（3）在第一象限的抛物线上是否存在一个点P，使得四边形ABPD的面积等于10？若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

分析 （1）设抛物线的顶点式，代入D的坐标，根据待定系数法求得即可；
（2）根据（1）求得的解析式，令y=0，求得A、B的坐标，根据图象即可求得；
（3）假设存在一个点P，使得四边形ABPD的面积等于10，求得直线BD的解析式，过P点作PE⊥AB于E，交DB于F，设P（x，-x²+2x+3），则F（x，-x+3），求得PF，然后根据S_△BPD=S_△PDF+S_△PFB=4，得到关于x的方程，解方程即可判断不存在x的值使方程成立，即可判定不存在这样的P点，使得四边形ABPD的面积等于10．

解答 解：（1）设抛物线的解析式为y=a（x-1）²+4，
代入D（0，3）得，3=a（0-1）²+4，解得a=-1，
∴y=-（x-1）²+4，
即此抛物线的解析式为y=-x²+2x+3；
（2）令y=0，则-x²+2x+3=0，
解得x₁=-1，x₂=3，
∴A（-1，0），B（3，0），
∵D（0，3），
∴不等式ax²+bx+c＞mx+n的解集为：0＜x＜3；
（3）不存在，
理由：假设存在一个点P，使得四边形ABPD的面积等于10，
∵A（-1，0），B（3，0），D（0，3），
∴AB=4，OD=3，
∴S_△ABD=$\frac{1}{2}$AB•OD=6，
∵四边形ABPD的面积等于10，
∴S_△BPD=10-6=4，
把B、D的坐标代入y=mx+n得$\left\{\begin{array}{l}{3m+n=0}\\{n=3}\end{array}\right.$，
解得$\left\{\begin{array}{l}{m=-1}\\{n=3}\end{array}\right.$，
∴直线BD的解析式为y=-x+3，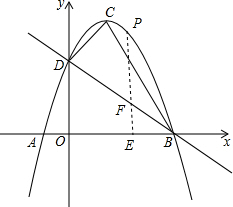
过P点作PE⊥AB于E，交DB于F，如图，
设P（x，-x²+2x+3），在F（x，-x+3），
∴CF=（-x²+2x+3）-（-x+3）=-x²+3x，
∴S_△BPD=S_△PDF+S_△PFB=$\frac{1}{2}$x（-x²+3x）+$\frac{1}{2}$（-x²+3x）•（3-x）=4，
整理得，3x²-9x+8=0，
∵△=（-9）²-4×3×8＜0，
∴不存在这样的P点，使得四边形ABPD的面积等于10．

点评 本题是二次函数的综合题，考查了待定系数法求二次函数的解析式，二次函数和不等式的关系以及四边形的面积等，（3）作出辅助线，把三角形分割成两个三角形是解题的关键．