题目内容
20．已知关于x的方程$\frac{x+a}{2}$-1=3x+4的解是不等式5x+7＞0的一个解，求a的取值范围．分析 通过解不等式得出x的取值范围，通过解方程得出a关于x的函数关系式，代入x的取值范围即可得出结论．
解答 解：解不等式：5x+7＞0，
得：x＞-$\frac{7}{5}$．
解方程：$\frac{x+a}{2}$-1=3x+4，
得：a=5x+10，
∵x＞-$\frac{7}{5}$，
∴a=5x+10＞5×（-$\frac{7}{5}$）+10=3．
∴a的取值范围为a＞3．
点评 本题考查了解一元一次不等式、一元一次方程的解以及一次函数的性质，解题的关键是得出a关于x的函数关系式．本题属于基础题，难度不大，解决该题型题目时，通过解方程得出a关于x的函数关系式是关键．
练习册系列答案
相关题目
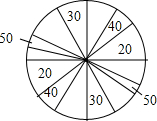某商场搞促销活动，规定凡购物满200元就有一次摇奖机会，摇奖的转盘如图所示．转盘上写有礼券金额，其中20元、30元、40元、50元礼券所对应的扇形的圆心角之和依次为80°、60°、40°、20°．计算：
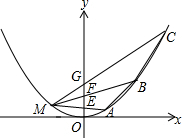如图，M、A，B，C为抛物线y=ax2上不同的四点，M（-2，1），线段MA，MB，MC与y轴的交点分别为E，F，G．且EF=FG=1．
解不等式组$\left\{\begin{array}{l}2x-1≤x+2，①\\ \frac{3x+1}{5}+2≥1．②\end{array}\right.$请结合题意填空，完成本题的解答．