题目内容
9. 解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.(Ⅰ)解不等式①,得x≤3;
(Ⅱ)解不等式②,得x≥-2;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为-2≤x≤3.
分析 (I)先移项,再合并同类项即可;
(II)先去分母,再移项,合并同类项,把x的系数化为1即可;
(III)把不等式①和②的解集在数轴上表示出来即可;
(IV)根据不等式①和②的解集即可得出不等式组的解集.
解答 解:(Ⅰ)移项得,2x-x≤2+1,
合并同类项得,x≤3.
故答案为:x≤3;
(Ⅱ)去分母得,3x+1+10≥5,
移项得,3x≥5-10-1,
合并同类项得,3x≥-6,
把x的系数化为1得,x≥-2.
故答案为:x≥-2;
(Ⅲ)在数轴上表示为: ;
;
(Ⅳ)由(III)知,不等式组的解集为:-2≤x≤3.
故答案为:-2≤x≤3.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
20.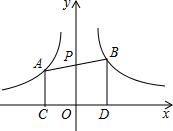 如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )
如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )
 如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )
如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )| A. | 3.5 | B. | 4 | C. | 4.5 | D. | 5 |
14.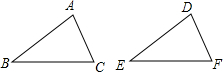 如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )
如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )
 如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )
如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
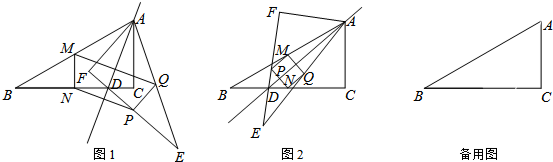
 如图,已知AB=AC,DE垂直平分AB,若∠A=40°,则∠EBC=30°.
如图,已知AB=AC,DE垂直平分AB,若∠A=40°,则∠EBC=30°.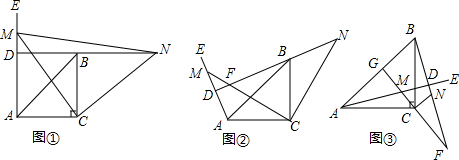
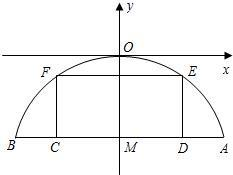 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.