Question

8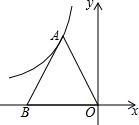．如图，反比例函数y=$\frac{k}{x}$（k≠0，x＜0）的图象过等边三角形AOB的顶点A（-1，$\sqrt{3}$），已知点B在x轴上．
（1）求反比例函数的表达式；
（2）若要使点B在上述反比例函数的图象上，需将△AOB向上平移多少个单位长度？

Answer 1

分析 （1）点A的坐标代入y=$\frac{k}{x}$（k≠0，x＜0），即可求得反比例函数的表达式；
（2）由当x=-2时，y=$\frac{\sqrt{3}}{2}$，则可得要使点B在上述反比例函数的图象上，需将△ABC向上平移$\frac{\sqrt{3}}{2}$个单位长度

解答 解：（1）∵反比例函数y=$\frac{k}{x}$（k≠0，x＜0）的图象过等边三角形AOB的顶点A（-1，$\sqrt{3}$），
∴k=-$\sqrt{3}$，
∴反比例函数的表达式为：y=-$\frac{\sqrt{3}}{x}$；

（2）∵△AOB是等边三角形，
∴B（-2，0），
∵当x=-2时，y=$\frac{\sqrt{3}}{2}$，
∴要使点B在上述反比例函数的图象上，需将△ABC向上平移$\frac{\sqrt{3}}{2}$个单位长度．

点评 本题考查了待定系数法求反比例函数的解析式、等边三角形的性质以及图象平移的性质．此题难度适中，注意掌握数形结合思想与方程思想的应用．