��Ŀ����
11����֪��ͬѧ���в������ŷֱ��������$\frac{1}{2}$��$\frac{1}{4}$��1�Ŀ�Ƭ����ͬѧ���в������ŷֱ��������1��3��2�Ŀ�Ƭ����Ƭ������ͬ���ִӼ����������и���ȡһ�ſ�Ƭ���������ǵ����ֱַ��Ϊa��b����1������������ͼ���б����г����п��ܵĽ����
��2�����ƶ�һ����Ϸ��������ѡ����a��b��ʹ��ax2+bx+1=0����������ȵ�ʵ���������ʤ�������һ�ʤ��������������Ϸ����ƽ�����ø���֪ʶ���ͣ�
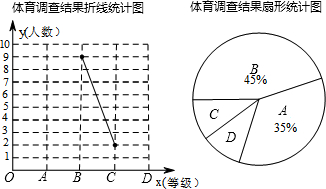
���� ��1�����ȸ������⻭����״ͼ��Ȼ������״ͼ������еȿ��ܵĽ����
��2������һԪ���η��̸����б�ʽ�������ж���������¸��������Ȼ�����ø��ʹ�ʽ��⼴����üס��һ�ʤ�ĸ��ʣ��Ƚϸ��ʴ�С������ȷ����������Ϸ���Ƿ�ƽ��
��� �⣺��1������״ͼ���£�
��ͼ��֪������9�ֵȿ��ܵĽ����
��2���ߣ�a��b���Ŀ��ܽ���У�$\frac{1}{2}$��1������$\frac{1}{2}$��3������$\frac{1}{2}$��2������$\frac{1}{4}$��1������$\frac{1}{4}$��3������$\frac{1}{4}$��2������1��1������1��3������1��2����
�൱a=$\frac{1}{2}$��b=1ʱ����=b2-4ac=-1��0����ʱax2+bx+1=0��ʵ������
��a=$\frac{1}{2}$��b=3ʱ����=b2-4ac=7��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a=$\frac{1}{2}$��b=2ʱ����=b2-4ac=2��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a=$\frac{1}{4}$��b=1ʱ����=b2-4ac=0����ʱax2+bx+1=0��������ȵ�ʵ������
��a=$\frac{1}{4}$��b=3ʱ����=b2-4ac=8��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a=$\frac{1}{4}$��b=2ʱ����=b2-4ac=3��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a=1��b=1ʱ����=b2-4ac=-3��0����ʱax2+bx+1=0��ʵ������
��a=1��b=3ʱ����=b2-4ac=5��0����ʱax2+bx+1=0����������ȵ�ʵ������
��a=1��b=2ʱ����=b2-4ac=0����ʱax2+bx+1=0��������ȵ�ʵ������
��P����ʤ��=P������0��=$\frac{5}{9}$��P���һ�ʤ��=1-$\frac{5}{9}$=$\frac{4}{9}$��
��P����ʤ����P���һ�ʤ����
����������Ϸ����Լ�����������ƽ��
���� ���⿼��������б�������״ͼ������ʣ�ע���б�������״ͼ�����Բ��ظ�����©���г����п��ܵĽ�����б����ʺ���������ɵ��¼�����״ͼ���ʺ�����������������ɵ��¼����õ���֪ʶ��Ϊ������=������������������֮�ȣ�

| A�� |  | B�� |  | C�� |  | D�� |  |
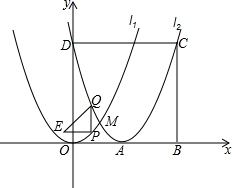 ��ͼ����AΪ�����������l2����������l1��y=x2��x������ƽ��2����λ��õ��ģ����������ཻ�ڵ�M��������l2��y�ύ�ڵ�D����ODΪ��������������ODCB��PΪ������l1��һ�㣬�������Ϊm��0��m��2�����ҵ�P�����M�غϣ�����P��PQ��y�ᣬ��������l2�ڵ�Q����PQ�Ƶ�P��ʱ����ת90�㣬�õ��߶�PE������EQ��
��ͼ����AΪ�����������l2����������l1��y=x2��x������ƽ��2����λ��õ��ģ����������ཻ�ڵ�M��������l2��y�ύ�ڵ�D����ODΪ��������������ODCB��PΪ������l1��һ�㣬�������Ϊm��0��m��2�����ҵ�P�����M�غϣ�����P��PQ��y�ᣬ��������l2�ڵ�Q����PQ�Ƶ�P��ʱ����ת90�㣬�õ��߶�PE������EQ��