题目内容
 正六边形的边长为8,则阴影部分的面积是多少?
正六边形的边长为8,则阴影部分的面积是多少?考点:正多边形和圆
专题:
分析:如图,作辅助线;首先证明△OAB、△OAC均为等边三角形,得到∠BAO=∠CAO=60°,借助扇形的面积公式和三角形的面积公式即可解决问题.
解答: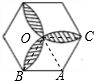 解:如图,连接OA、OB、OC;
解:如图,连接OA、OB、OC;
由题意知:∠BOA=∠COA=
×360°=60°,
∵OA=OB=OC,
∴△OAB、△OAC均为等边三角形,
∴∠BAO=∠CAO=60°,
S扇形ABO+S扇形AOC=
×2=
;
S△ABO+S△ACO=
×82×sin60°×2=32
,
∴阴影部分的面积=3×(
-32
)=64π-96
.
 解:如图,连接OA、OB、OC;
解:如图,连接OA、OB、OC;由题意知:∠BOA=∠COA=
| 1 |
| 6 |
∵OA=OB=OC,
∴△OAB、△OAC均为等边三角形,
∴∠BAO=∠CAO=60°,
S扇形ABO+S扇形AOC=
| 60π•82 |
| 360 |
| 64π |
| 3 |
S△ABO+S△ACO=
| 1 |
| 2 |
| 3 |
∴阴影部分的面积=3×(
| 64π |
| 3 |
| 3 |
| 3 |
点评:该题主要考查了正多边形和圆的性质及其应用问题;解题的关键是灵活运用正多边形和圆的性质来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
相关题目
 如图,△ABC中,M为AC边的中点,E为AB上一点,且AE=
如图,△ABC中,M为AC边的中点,E为AB上一点,且AE= 如图,已知∠A=∠C,∠1与∠2互补,若∠1=∠C,请直接写出所有与∠A相等的角.
如图,已知∠A=∠C,∠1与∠2互补,若∠1=∠C,请直接写出所有与∠A相等的角.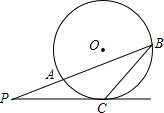 如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.
如图,已知P是⊙O外一点,从P引两条射线,分别与⊙O交于A、B及C,且PC2=PA•PB,求证:PC是⊙O的切线.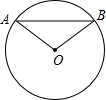 如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值.
如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值.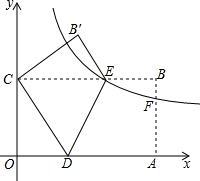 如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、B才边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.
如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、B才边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.