题目内容
已知:在△ACB中,∠ACB=90°,M是AB中点,MD⊥AB交AC于E,交BC的延长线于D,求证:AB2=4ME•MD.
考点:相似三角形的判定与性质
专题:证明题
分析:作出图形,易证∠A=∠D,再根据∠AME=∠DMB=90°即可证明△AME∽△DME,可得
=
,整理得:AM•BM=ME•MD,再根据AM=BM=
AB,即可解题.
| AM |
| ME |
| DM |
| BM |
| 1 |
| 2 |
解答:证明:作出图形,

∵∠A+∠AEM=90°,∠D+∠DEC=90°,∠DEC=∠AEM,
∴∠A=∠D,
∵∠AME=∠DMB=90°,
∴△AME∽△DME,
∴
=
,
∴AM•BM=ME•MD,
∵M是AB中点,
∴AM=BM=
AB,
∴
AB2=ME•MD,
∴AB2=4ME•MD.

∵∠A+∠AEM=90°,∠D+∠DEC=90°,∠DEC=∠AEM,
∴∠A=∠D,
∵∠AME=∠DMB=90°,
∴△AME∽△DME,
∴
| AM |
| ME |
| DM |
| BM |
∴AM•BM=ME•MD,
∵M是AB中点,
∴AM=BM=
| 1 |
| 2 |
∴
| 1 |
| 4 |
∴AB2=4ME•MD.
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,本题中求证△AME∽△DME是解题的关键.

练习册系列答案
相关题目
若有理数a、b满足|a|=|b|,则下列各式中正确的是( )
| A、a=b |
| B、a=-b |
| C、a2=|b| |
| D、a2=b2 |
下面结论不正确的是( )
| A、两点确定一条直线 |
| B、两点之间,线段最短 |
| C、锐角的补角相等 |
| D、等角的余角相等 |
 正六边形的边长为8,则阴影部分的面积是多少?
正六边形的边长为8,则阴影部分的面积是多少?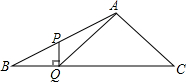 在△ABC中,∠B=30°,P为AB上的一点,
在△ABC中,∠B=30°,P为AB上的一点,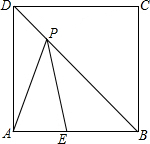 已知:如图,正方形ABCD的边长为6
已知:如图,正方形ABCD的边长为6