题目内容
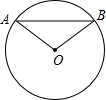 如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值.
如图,已知⊙O的半径为30mm,弦AB=36mm,求点O到AB的距离及∠OAB的余弦值.考点:垂径定理,解直角三角形
专题:
分析:作OC⊥AB,根据等腰三角形底边三线合一的性质即可求得C是AB中点,即可求得AC的值,即可求得cos∠OAB的值,根据勾股定理即可求得OC的值,即可解题.
解答:解:作OC⊥AB,

∵OA=OB,
∴△OAB是等腰三角形,
∴C是AB中点,
∴cos∠OAB=
=
,
∵CO2=AO2-AC2=576cm2,
∴CO=24cm.
∴点O到AB的距离为24cm.

∵OA=OB,
∴△OAB是等腰三角形,
∴C是AB中点,
∴cos∠OAB=
| ||
| AO |
| 3 |
| 5 |
∵CO2=AO2-AC2=576cm2,
∴CO=24cm.
∴点O到AB的距离为24cm.
点评:本题考查了垂径定理,考查了等腰三角形底边三线合一的性质,考查了直角三角形中勾股定理的运用,本题中根据垂径定理求得AC的长是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
“神舟十号”从地球出发飞行38万公里进入绕月轨道,用科学记数法表示飞行距离为( )
| A、0.38×106公里 |
| B、3.8×105公里 |
| C、38×104公里 |
| D、3.8×104公里 |
若有理数a、b满足|a|=|b|,则下列各式中正确的是( )
| A、a=b |
| B、a=-b |
| C、a2=|b| |
| D、a2=b2 |
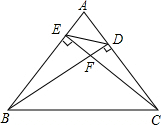 如图,BD、CE是△ABC的高.
如图,BD、CE是△ABC的高. 正六边形的边长为8,则阴影部分的面积是多少?
正六边形的边长为8,则阴影部分的面积是多少?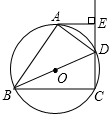 如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.
如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD,垂足为E,DA平分∠BDE.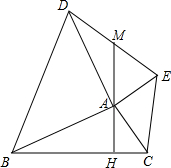 如图,在△ABC外作等腰直角△ABD与等腰直角△ACE,使得∠BAD=90°,∠CAE=90°,AH⊥BC,垂足为H,AH的反向延长线交DE于M,求证:DM=EM.
如图,在△ABC外作等腰直角△ABD与等腰直角△ACE,使得∠BAD=90°,∠CAE=90°,AH⊥BC,垂足为H,AH的反向延长线交DE于M,求证:DM=EM. 已知:如图,正方形ABCD的边长为6
已知:如图,正方形ABCD的边长为6