题目内容
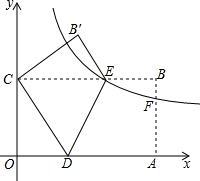 如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、B才边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.
如图,在平面直角坐标系中,A(16,0)、C(0,8),四边形OABC是矩形,D、E分别是OA、B才边上的点,沿着DE折叠矩形,点A恰好落在y轴上的点C处,点B落在点B′处.(1)求D、E两点的坐标;
(2)点F是矩形的AB边上的点,且EF=3
| 5 |
考点:反比例函数综合题
专题:
分析:(1)设OD=m,则CD=DA=16-m,在Rt△COD中,由勾股定理可得m=6,即可得D的坐标,再根据矩形的性质,可得CE=CD=10,可得E的坐标;
(2)过B′作B′M⊥BC于M,易得B′M与CM的长,进而可得反比例函数解析式,易求点F的坐标;根据题意,分三种情况讨论,可得在平面直角坐标系中存在G1、G2、G3的坐标,进而可得答案.
(2)过B′作B′M⊥BC于M,易得B′M与CM的长,进而可得反比例函数解析式,易求点F的坐标;根据题意,分三种情况讨论,可得在平面直角坐标系中存在G1、G2、G3的坐标,进而可得答案.
解答: 解:(1)∵A(16,0)、C(0,8),
解:(1)∵A(16,0)、C(0,8),
∴OA=16,OC=8,
设OD=m,则CD=DA=16-m.
在Rt△COD中,∠COD=90°.
∵CD2=OC2+OD2,
∴(16-m)2=82+m2,
解得m=6,
∴D(6,0).
∵四边形OABC是矩形,
∴OA∥CB,
∴∠CED=∠EDA,
∵∠EDA=∠CDE,
∴∠CED=∠CDE,
∴CE=CD=10,
∴E(10,8);
(2)设过点E、F的双曲线解析式为:y=
(k≠0).
如图1,过B′作B′M⊥BC于M
∵B′C=AB=8,B′E=BE=6,∠CB′E=90°
∴B′M=
=
=4.8
CM=
=6.4,B′(6.4,12.8)
∵k=10×8=80,
∴y=
.
故设F(x,
).
∵EF=3
,E(10,8),
∴(10-x)2+(8-
)2=45.
解得 x=16,则y=5,
∴F(16,5),有三种情况如图2:
①把线段DE先向右平移10个单位长度,再向上平移5个单位,端点E落在G1处,G1(20,13);
②把线段EF先向左平移4个单位长度,再向下平移8个单位,端点F落在G2处,G2(12,-3);
③把线段DF先向左平移6个单位长度,再向上平移3个单位,端点D落在G3处,G3(0,3).
综上所述,在平面直角坐标系中存在G1(20,13)、G2(12,-3)、G3(0,3)使得以点D、E、F、G为顶点的四边形是平行四边形.
 解:(1)∵A(16,0)、C(0,8),
解:(1)∵A(16,0)、C(0,8),∴OA=16,OC=8,
设OD=m,则CD=DA=16-m.
在Rt△COD中,∠COD=90°.
∵CD2=OC2+OD2,
∴(16-m)2=82+m2,
解得m=6,
∴D(6,0).
∵四边形OABC是矩形,
∴OA∥CB,
∴∠CED=∠EDA,
∵∠EDA=∠CDE,
∴∠CED=∠CDE,
∴CE=CD=10,
∴E(10,8);
(2)设过点E、F的双曲线解析式为:y=
| k |
| x |
如图1,过B′作B′M⊥BC于M

∵B′C=AB=8,B′E=BE=6,∠CB′E=90°
∴B′M=
| CB×B′E |
| CE |
| 8×6 |
| 10 |
CM=
| B′C2-B′M2 |
∵k=10×8=80,
∴y=
| 80 |
| x |
故设F(x,
| 80 |
| x |
∵EF=3
| 5 |
∴(10-x)2+(8-
| 80 |
| x |
解得 x=16,则y=5,
∴F(16,5),有三种情况如图2:
①把线段DE先向右平移10个单位长度,再向上平移5个单位,端点E落在G1处,G1(20,13);
②把线段EF先向左平移4个单位长度,再向下平移8个单位,端点F落在G2处,G2(12,-3);
③把线段DF先向左平移6个单位长度,再向上平移3个单位,端点D落在G3处,G3(0,3).
综上所述,在平面直角坐标系中存在G1(20,13)、G2(12,-3)、G3(0,3)使得以点D、E、F、G为顶点的四边形是平行四边形.
点评:本题考查了反比例函数的图象的性质以及其与直线的关系,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
若有理数a、b满足|a|=|b|,则下列各式中正确的是( )
| A、a=b |
| B、a=-b |
| C、a2=|b| |
| D、a2=b2 |
下面结论不正确的是( )
| A、两点确定一条直线 |
| B、两点之间,线段最短 |
| C、锐角的补角相等 |
| D、等角的余角相等 |
 如图,在矩形ABCD中,AB=3cm,BC=4cm,△ABC沿AC翻折后点B落在B′,B′C与AD相交于点E,求△AEC的面积.
如图,在矩形ABCD中,AB=3cm,BC=4cm,△ABC沿AC翻折后点B落在B′,B′C与AD相交于点E,求△AEC的面积. 正六边形的边长为8,则阴影部分的面积是多少?
正六边形的边长为8,则阴影部分的面积是多少?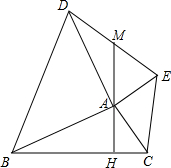 如图,在△ABC外作等腰直角△ABD与等腰直角△ACE,使得∠BAD=90°,∠CAE=90°,AH⊥BC,垂足为H,AH的反向延长线交DE于M,求证:DM=EM.
如图,在△ABC外作等腰直角△ABD与等腰直角△ACE,使得∠BAD=90°,∠CAE=90°,AH⊥BC,垂足为H,AH的反向延长线交DE于M,求证:DM=EM.