Question

9．如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴，y轴上，连结OB，将纸片OABC沿OB对折，使点A落在点E的位置，若OB=$\sqrt{5}$，tan∠BOC=$\frac{1}{2}$，则点E的坐标为（　　）

• A． （-$\frac{4}{5}，\frac{3}{5}$）
• B． （-$\frac{3}{5}，\frac{4}{5}$）
• C． （-1，1）
• D． （-1，2）

Answer 1

分析 过点E作ED⊥x轴与点D，根据题意首先求出AB、BC的长度；借助面积公式求出ED、OD的长度，即可解决问题．

解答 解：如图，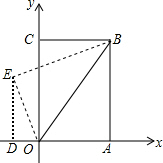

过点E作ED⊥x轴与点D；
设ED=x，OD=y；
∵四边形ABCO为矩形，
∴∠OAB=∠OCB=90°；四边形ABED为梯形；
设AB=OC=a，BC=AO=b；
∵OB=$\sqrt{5}$，tan∠BOC=$\frac{1}{2}$，
∴$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=5}\\{\frac{b}{a}=\frac{1}{2}}\end{array}\right.$，
解得：a=2，b=1；
由题意得：EO=AO=1；△ABO≌△EBO；
由勾股定理得：x²+y²=1①，
由面积公式得：$\frac{1}{2}$xy+2×$\frac{1}{2}$×2×1=$\frac{1}{2}$（x+2）（y+1）②；
联立①②并解得：x=$\frac{4}{5}$，y=$\frac{3}{5}$，
则点E的坐标为（-$\frac{3}{5}$，$\frac{4}{5}$）．
故选：B．

点评 此题考查翻折变换，坐标与图形的性质；综合利用矩形的性质、三角函数的定义、勾股定理等几何知识点解决问题．