题目内容
4.有10个正实数,这些数中每两个乘积恰好为1,这时甲同学断言,任何9个数的和不小于$\sqrt{2}$;乙同学断言:任何9个数的和小于$\sqrt{2}$,则两位同学甲正确.分析 由每两个乘积恰好为1,判断任意两数互为倒数,任意9数的和列出代数式,根据a2+b2≥2ab从而确定和的范围.
解答 解:∵这些数中每两个乘积恰好为1,且都是正数,
∴任意两个数互为倒数,
故可设这两数分别为x,$\frac{1}{x}$(x>0,$\frac{1}{x}$>0),且x•$\frac{1}{x}$=1;
根据题意,任意9个数的和为:
①$4(x+\frac{1}{x})+x$=5x+$\frac{4}{x}$≥2$\sqrt{5x•\frac{4}{x}}$=4$\sqrt{5}$;
②$4(x+\frac{1}{x})+\frac{1}{x}$=4x+$\frac{5}{x}$≥2$\sqrt{4x•\frac{5}{x}}$=4$\sqrt{5}$;
∵4$\sqrt{5}$>$\sqrt{2}$,
∴任意9个数的和不小于$\sqrt{2}$.
故答案为:甲.
点评 本题主要考查倒数的性质及a2+b2≥2ab的应用,根据题意列出代数式并确定范围是关键.

练习册系列答案
相关题目
12.已知等式ax=ay,下列变形不正确的是( )
| A. | x=y | B. | ax+1=ay+1 | C. | 2ax=2ay | D. | 3-ax=3-ay |
19. 如图,在△ABC中,AB=AC,∠A=30°,以C为圆心,CB的长为半径作圆弧,交AB于点D,连接CD,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=30°,以C为圆心,CB的长为半径作圆弧,交AB于点D,连接CD,则∠ACD等于( )
 如图,在△ABC中,AB=AC,∠A=30°,以C为圆心,CB的长为半径作圆弧,交AB于点D,连接CD,则∠ACD等于( )
如图,在△ABC中,AB=AC,∠A=30°,以C为圆心,CB的长为半径作圆弧,交AB于点D,连接CD,则∠ACD等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
9. 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )
 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )| A. | (-$\frac{4}{5},\frac{3}{5}$) | B. | (-$\frac{3}{5},\frac{4}{5}$) | C. | (-1,1) | D. | (-1,2) |
 如图,在△ABC中,∠BAC=90°,AB=AC,∠ABD=∠BAD=15°,求证:AC=DC.
如图,在△ABC中,∠BAC=90°,AB=AC,∠ABD=∠BAD=15°,求证:AC=DC. 已知:如图,AB是⊙O的直径,直线l交⊙O于C、D两点,AE⊥l,BF⊥l,E、F是垂足,求证:EC=DF.
已知:如图,AB是⊙O的直径,直线l交⊙O于C、D两点,AE⊥l,BF⊥l,E、F是垂足,求证:EC=DF.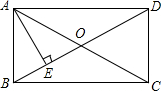 如图,在矩形ABCD中,AE⊥BD于E,AC与BD相交于O点,DE=3BE.
如图,在矩形ABCD中,AE⊥BD于E,AC与BD相交于O点,DE=3BE.