题目内容
18. 如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.
如图,在ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.(1)作△ACD外接圆⊙O(尺规作图,保留作图痕迹,不写作法);
(2)判断直线BC与⊙O的位置关系,并证明你的结论.
分析 (1)先作线段AD的垂直平分线交AD于O点,然后以O为圆心,OA为半径画圆即可;
(2)连接CO,如图,利用三角形外角性质得到∠COB=2∠A=60°,则∠COB+∠B=90°,所以∠OCB=90°,然后根据切线的判定定理可判断BC与⊙O相切.
解答 解:(1)如图,⊙O为所作;
(2)BC与⊙O相切.
证明如下:连接CO,如图,
∵∠A=∠B=30°,
∴∠COB=2∠A=60°,
∴∠COB+∠B=30°+60°=90°,
∴∠OCB=90°,
∴OC⊥BC,
又BC经过半径OC的外端点C,
∴BC与⊙O相切.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了切线的判定定理.

练习册系列答案
相关题目
9. 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )
 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )| A. | (-$\frac{4}{5},\frac{3}{5}$) | B. | (-$\frac{3}{5},\frac{4}{5}$) | C. | (-1,1) | D. | (-1,2) |
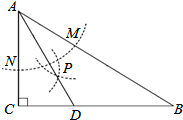 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( ) 为迎接省卫生文明城市建设,某校把一块形状为直角三角形的废地开辟为植物园.如图所示,∠ACB=90°,AC=80m,BC=60m.若线段CD是一条水渠,且CD⊥AB,已知水渠的造价为100元/m,求水渠CD的长及其造价.
为迎接省卫生文明城市建设,某校把一块形状为直角三角形的废地开辟为植物园.如图所示,∠ACB=90°,AC=80m,BC=60m.若线段CD是一条水渠,且CD⊥AB,已知水渠的造价为100元/m,求水渠CD的长及其造价.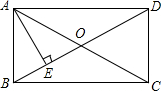 如图,在矩形ABCD中,AE⊥BD于E,AC与BD相交于O点,DE=3BE.
如图,在矩形ABCD中,AE⊥BD于E,AC与BD相交于O点,DE=3BE. 如图,在△ABC中,∠C=90°,按以下步骤作图:
如图,在△ABC中,∠C=90°,按以下步骤作图: 已知:如图,把菱形ABCD沿着AC方向平移得到菱形A1B1C1D1,BC与A1B1相交于点E,DC与A1D1相交于点F.求证:四边形A1ECF是菱形.
已知:如图,把菱形ABCD沿着AC方向平移得到菱形A1B1C1D1,BC与A1B1相交于点E,DC与A1D1相交于点F.求证:四边形A1ECF是菱形. 如图.在△ABC中.AB=10,AC=6,BC=8,AD平分∠BAC交BC于点F,且△ABC≌△ADE,求图中阴影部分的面积.
如图.在△ABC中.AB=10,AC=6,BC=8,AD平分∠BAC交BC于点F,且△ABC≌△ADE,求图中阴影部分的面积. 如图,AB、CD是⊙O的两条弦,AB⊥CD,垂足为点M,AM=4,BM=6,CM=3,DM=8,求⊙O的半径.
如图,AB、CD是⊙O的两条弦,AB⊥CD,垂足为点M,AM=4,BM=6,CM=3,DM=8,求⊙O的半径.