题目内容
19. 如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F,若∠E=∠F=35°,则∠A的度数是( )
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F,若∠E=∠F=35°,则∠A的度数是( )| A. | 35° | B. | 55° | C. | 60° | D. | 65° |
分析 由∠E=∠F=35°,利用三角形外角的性质,易证得∠ADC=∠ABC,又由圆的内接四边形的性质,证得∠ADC+∠ABC=180°,继而求得∠ABC的度数,然后由三角形内角和定理,求得答案.
解答 解:∵∠ADC=∠E+∠ECD,∠ABC=∠F+∠BCF,且∠E=∠F=35°,∠DCF=∠BCF,
∴∠ADC=∠ABC,
∵四边形ABCD内接⊙O,
∴∠ADC+∠ABC=180°,
∴∠ABC=90°,
∴∠A=90°-∠E=55°.
故选B.
点评 此题考查了圆的内接四边形的性质.注意求得∠ABC=90°是解此题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10. 如图,正方形ABCD绕D旋转90°到了正方形CDEF处,那么旋转方向是( )
如图,正方形ABCD绕D旋转90°到了正方形CDEF处,那么旋转方向是( )
 如图,正方形ABCD绕D旋转90°到了正方形CDEF处,那么旋转方向是( )
如图,正方形ABCD绕D旋转90°到了正方形CDEF处,那么旋转方向是( )| A. | 逆时针 | B. | 顺时针 | C. | 顺时针或逆时针 | D. | 无法确定 |
9. 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )
 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )
如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴,y轴上,连结OB,将纸片OABC沿OB对折,使点A落在点E的位置,若OB=$\sqrt{5}$,tan∠BOC=$\frac{1}{2}$,则点E的坐标为( )| A. | (-$\frac{4}{5},\frac{3}{5}$) | B. | (-$\frac{3}{5},\frac{4}{5}$) | C. | (-1,1) | D. | (-1,2) |
 如图所示,△ABC中,AB=AC,E是AB上一点,F在AC的延长线上,BE=CF,连接EF交BC于D,过E作EG∥AF交BC于G.
如图所示,△ABC中,AB=AC,E是AB上一点,F在AC的延长线上,BE=CF,连接EF交BC于D,过E作EG∥AF交BC于G. 如图,在△ABC中,∠BAC=90°,AB=AC,∠ABD=∠BAD=15°,求证:AC=DC.
如图,在△ABC中,∠BAC=90°,AB=AC,∠ABD=∠BAD=15°,求证:AC=DC. 如图是一个横断面为抛物线形状的拱桥,当水面宽8米时,拱顶(拱桥洞的最高点)离水面4m,水面上升1m时,水面的宽度为$4\sqrt{3}$.
如图是一个横断面为抛物线形状的拱桥,当水面宽8米时,拱顶(拱桥洞的最高点)离水面4m,水面上升1m时,水面的宽度为$4\sqrt{3}$.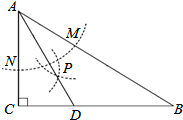 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )