题目内容
9.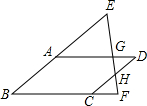 如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )
如图,四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD,CD于点G,H,则下列结论错误的是( )| A. | $\frac{EA}{BE}$=$\frac{EG}{EF}$ | B. | $\frac{EG}{GH}$=$\frac{AG}{GD}$ | C. | $\frac{AB}{AE}$=$\frac{BC}{CF}$ | D. | $\frac{FH}{EH}$=$\frac{CF}{AD}$ |
分析 根据相似三角形的判定和性质进行判断即可.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BF,BE∥DC,AD=BC,
∴$\frac{EA}{BE}=\frac{EG}{EF}$,$\frac{EG}{GH}=\frac{AG}{GD}$,$\frac{HF}{EH}=\frac{FC}{BC}=\frac{CF}{AD}$,
故选C.
点评 此题考查相似三角形的判定和性质,关键是根据相似三角形的判定和性质来分析判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.实数-$\frac{1}{2}$的相反数是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
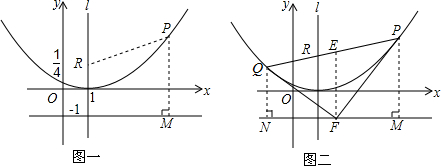
 如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC=$\frac{3}{2}$.
如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC=$\frac{3}{2}$.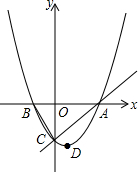 如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
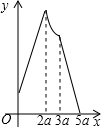
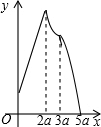
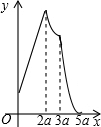
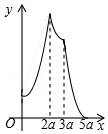
如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.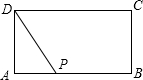 如图,在矩形ABCD中,AB=2a,AD=a,矩形边上一动点P沿A→B→C→D的路径移动.设点P经过的路径长为x,PD2=y,则下列能大致反映y与x的函数关系的图象是( )
如图,在矩形ABCD中,AB=2a,AD=a,矩形边上一动点P沿A→B→C→D的路径移动.设点P经过的路径长为x,PD2=y,则下列能大致反映y与x的函数关系的图象是( )